TRNG BASICS: True Random Number Generator mit dem GDK-101 Gamma Strahlen Detektor und dem Raspberry Pi Pico

Die Welt, wie wir sie kennen, scheint durch Gesetze und Regeln geordnet zu sein. Wir beobachten regelmäßige Bewegungen der Himmelskörper, das beständige Fließen von Flüssen und die vorhersehbare Wirkung der Schwerkraft. Die physikalischen Gesetze, die wir aus diesen Beobachtungen ableiten, erlauben uns, Voraussagen zu treffen und die Welt um uns herum zu verstehen. In dieser Welt scheint auf den ersten Blick wenig Platz für den Zufall zu sein.

Und doch, wenn wir tiefer in das Wesen der Realität eintauchen, in die Welt der kleinsten Teilchen, stoßen wir auf ein Phänomen, das unserer Alltagserfahrung widerspricht – den Zufall. Die Quantenmechanik, ein Eckpfeiler unserer modernen physikalischen Theorie, ist durchdrungen von Zufälligkeit und Unvorhersehbarkeit. Ein zentrales Beispiel hierfür ist der radioaktive Zerfall, bei dem wir lediglich die Wahrscheinlichkeit angeben können, dass ein Atom innerhalb eines bestimmten Zeitraums zerfällt, jedoch nicht, wann es genau geschehen wird.

Diese fundamentale Zufälligkeit wirft tiefgründige Fragen auf, die sowohl die Physik als auch die Philosophie betreffen. Was bedeutet es für unsere Sicht auf das Universum, wenn wir akzeptieren, dass bestimmte Ereignisse grundlegend zufällig sind? Wie passt dies zu unserem Verständnis von Kausalität und Determinismus?

Der Dämon des Determinismus

Laplace’s Dämon ist ein Gedankenexperiment, das vom französischen Mathematiker und Physiker Pierre-Simon Laplace im 19. Jahrhundert vorgeschlagen wurde. Es dient als ein Modell für wissenschaftlichen Determinismus, eine Ansicht, die besagt, dass der Zustand des Universums zu einem bestimmten Zeitpunkt vollständig durch den Zustand zu jedem anderen Zeitpunkt bestimmt ist.

Laplace stellte sich einen „Dämon“ vor – ein Wesen mit unendlicher Rechenkraft und vollständigem Wissen über die Position und Geschwindigkeit jedes einzelnen Teilchens im Universum. Laut Laplace könnte dieser Dämon, wenn er alle Kräfte kennt, die die Natur ins Spiel bringt, und den Zustand aller Entitäten zu einem bestimmten Zeitpunkt, die Bewegungen der größten Körper im Universum und die des leichtesten Atoms berechnen; nichts wäre für ihn ungewiss, und die Zukunft, wie die Vergangenheit, wäre gegenwärtig in seinen Augen.

Dieses Konzept unterstreicht die Vorstellung des klassischen Determinismus: Wenn wir genug Informationen über den Zustand des Universums und genügend Rechenkraft hätten, könnten wir in Theorie das gesamte zukünftige (und vergangene) Verhalten des Universums vorhersagen.

Das Konzept des Laplace’schen Dämons, wenn es vollständig realisiert werden könnte, hätte mehrere weitreichende Konsequenzen:

1. Vollständiger Determinismus: Wenn alle Bewegungen und Zustände im Universum vorhersehbar sind, dann bedeutet das, dass das Universum völlig deterministisch ist. Es gibt keinen Zufall oder Unvorhersehbarkeit auf einer fundamentalen Ebene; alles, was passiert, ist das Ergebnis von bestimmten Gesetzen und initialen Bedingungen.
2. Kein Freier Wille: In einem vollständig deterministischen Universum ist das Konzept des freien Willens problematisch. Wenn jede Aktion, die wir ausführen, einschließlich unserer Gedanken und Entscheidungen, das Ergebnis von physikalischen Gesetzen ist, dann sind sie im Grunde vorherbestimmt und nicht das Ergebnis einer freien Wahl.
3. Zeitreisen: In gewisser Weise impliziert das Konzept des Laplace’schen Dämons die Möglichkeit von „Zeitreisen“ – nicht in dem Sinne, dass man physisch in die Vergangenheit oder Zukunft reisen könnte, sondern in dem Sinne, dass man die Vergangenheit vollständig rekonstruieren und die Zukunft vorhersagen könnte, wenn man genügend Informationen und Rechenkraft hätte.
4. Verlust der Privatsphäre: In einem hypothetischen Szenario, in dem ein Laplace’scher Dämon existieren könnte, würde es keine Privatsphäre geben. Jede Handlung, jeder Gedanke und jedes zukünftige Ereignis könnte im Voraus bekannt sein.

Eine schaurige Vorstellung…

Quantentheorie: Rettung des Zufalls?

Die Quantenmechanik, die im 20. Jahrhundert entwickelt wurde, wirft ernsthafte Fragen über die Idee des Laplace’schen Dämons auf. Insbesondere das Heisenbergsche Unschärferelationsprinzip stellt fest, dass es unmöglich ist, gleichzeitig den genauen Ort und die genaue Geschwindigkeit eines Teilchens zu kennen. Diese Theorie, die auf der mikroskopischen Ebene arbeitet – die Welt der Atome und subatomaren Partikel, ist geprägt von einer inhärenten Zufälligkeit. Dies steht im direkten Widerspruch zu den Annahmen, die der Vorstellung des Laplace’schen Dämons zugrunde liegen.

Die Heisenbergsche Unschärferelation ist ein grundlegendes Prinzip der Quantenmechanik, das besagt, dass es unmöglich ist, gleichzeitig die genaue Position und den genauen Impuls (ein Maß für Geschwindigkeit und Masse) eines Teilchens zu kennen. Je genauer wir die Position kennen, desto unsicherer sind wir über den Impuls und umgekehrt.

Diese Unschärfe ist kein Resultat mangelnder Messgenauigkeit oder technischer Beschränkungen, sondern eine fundamentale Eigenschaft der Natur auf der Quantenebene. Das heißt, die Unschärfe ist nicht einfach ein „Problem“, das durch bessere Messgeräte oder ausgeklügeltere Techniken behoben werden könnte. Sie ist eine intrinsische Eigenschaft der Quantenwelt und bringt eine grundlegende Unvorhersehbarkeit mit sich.

Bezogen auf die Frage nach dem Zufall ergibt sich hieraus eine interessante Schlussfolgerung. Da wir nicht genau bestimmen können, wo ein Teilchen ist und wie schnell es sich bewegt, können wir auch nicht genau vorhersagen, wo es sich in der Zukunft befinden wird. In diesem Sinne führt die Unschärferelation zu einer Art quantenmechanischer „Zufälligkeit“ oder Unvorhersehbarkeit.

Es ist jedoch wichtig zu betonen, dass diese Art von Zufälligkeit nicht das ist, was wir uns normalerweise unter „Zufall“ vorstellen. Es ist keine Frage von Unwissenheit oder mangelnder Information. Vielmehr ist es eine fundamentale Unbestimmtheit, die in der Natur der Quantenwelt selbst verankert ist.

Die Quantenmechanik erlaubt uns nur, die Wahrscheinlichkeitsverteilung eines Teilchenzustands zu berechnen, was bedeutet, dass wir nur Aussagen über die Wahrscheinlichkeit von Ergebnissen machen können, nicht über spezifische Einzelergebnisse. Daher führt die Quantenunschärfe zu einer grundlegenden zufälligen Natur der mikroskopischen Welt.

Ein markantes Beispiel für diesen intrinsischen Zufall ist der Zerfall eines Atoms. Bei einem instabilen Atom können wir nicht vorhersagen, wann es zerfällt. Es gibt keine äußeren Faktoren oder „Auslöser“, die den Zerfall verursachen. Stattdessen können wir nur die Wahrscheinlichkeit angeben, dass ein Atom innerhalb eines bestimmten Zeitraums zerfällt. Jeder einzelne Atomzerfall ist ein eindeutig zufälliges Ereignis. Während die Physiker dieses Phänomen exakt beschreiben und vorhersagen können, wie viele Atome in einer großen Menge im Durchschnitt zerfallen werden, können sie nicht vorhersagen, wann ein bestimmtes Atom zerfallen wird.

Dieser inhärente Zufall auf Quantenebene hat tiefgreifende philosophische Auswirkungen und fordert unsere traditionellen Ansichten von Kausalität und Determinismus heraus. Philosophisch gesehen war der Zufall schon immer ein strittiges Konzept. Die Stoiker beispielsweise lehnten die Idee des Zufalls ab und glaubten stattdessen an ein universelles Netz der Kausalität. Andere Philosophen, wie David Hume, argumentierten, dass das, was wir als Zufall bezeichnen, oft nur unsere Unkenntnis über die zugrundeliegenden Ursachen ist. Mit der Quantenmechanik jedoch erhielt der Zufall eine wissenschaftliche Grundlage.

Wie lässt sich dieser Ansatz nutzen um einen „echten“ Zufallsgenerator zu erzeugen?

Die Unmöglichkeit, den genauen Zeitpunkt des Zerfalls eines bestimmten Atoms vorherzusagen, ist eine direkte Folge der Prinzipien der Quantenmechanik. Dies unterscheidet sich grundlegend von der Unvorhersehbarkeit in der klassischen Physik, die oft aus unserem Mangel an vollständigem Wissen oder der Unfähigkeit zur Berechnung komplexer Systeme resultiert.

Im Zentrum der Quantenmechanik steht die Wellenfunktion, eine mathematische Funktion, die die Wahrscheinlichkeiten für den Zustand eines Quantensystems repräsentiert. Bis eine Messung durchgeführt wird, können Teilchen in einer Überlagerung von Zuständen existieren. Die Messung „kollabiert“ die Wellenfunktion in einen bestimmten Zustand.

Im Falle des radioaktiven Zerfalls kann die Wahrscheinlichkeit, dass ein Atom in einem bestimmten Zeitraum zerfällt, durch die Wellenfunktion des Atoms und die Zeitabhängige Schrödinger-Gleichung berechnet werden. Diese Wahrscheinlichkeit ist jedoch das einzige, was wir wissen können. Es gibt keinen Weg, vorherzusagen, wann ein spezifisches Atom genau zerfallen wird. Dies ist eine inhärente Unbestimmtheit, die Teil der grundlegenden Struktur der Quantenmechanik ist.

Dies ist ein beeindruckendes Beispiel für das, was Albert Einstein so störte, dass er das berühmte Zitat prägte: „Gott würfelt nicht.“ Aber im Bereich der Quantenmechanik scheint es, als ob zumindest ein Teil der Natur durch zufällige Prozesse bestimmt ist.

Und wenn es doch ein zugrundeliegenden Prinzip gibt, welches wir nur noch nicht erkennen?

Die Vorstellung, dass die scheinbare Zufälligkeit in der Quantenmechanik tatsächlich auf unserer Unkenntnis über tiefere, noch unbekannte physikalische Prinzipien beruht, ist eine philosophische Position, die als „verborgene Variablen-Theorie“ bekannt ist. Sie geht davon aus, dass die Quantenmechanik nicht die ganze Geschichte erzählt und dass es zusätzliche „verborgene Variablen“ gibt, die, wenn sie einmal entdeckt sind, die Quantenphänomene vollständig und deterministisch erklären könnten.

Allerdings liefert das berühmte Bell-Theorem wichtige Einschränkungen für die Art von verborgenen Variablen-Theorien, die mit der Quantenmechanik kompatibel sein könnten. John Bell zeigte 1964, dass wenn solche verborgenen Variablen existieren, sie entweder nicht lokal sein müssen (das heißt, sie müssten eine sofortige, „spukhafte“ Wirkung über große Entfernungen haben, die mit der speziellen Relativitätstheorie unvereinbar ist), oder sie müssen kontextabhängig sein (das heißt, die Ergebnisse von Messungen würden von Faktoren abhängen, die sie prinzipiell nicht beeinflussen sollten). Experimente, die auf Bells Theorem basieren, haben starke Beweise dafür geliefert, dass die Quantenmechanik tatsächlich nicht lokal ist, was die meisten einfachen verborgenen Variablen-Theorien ausschließt.

Es ist jedoch immer noch möglich, dass es eine tiefere Theorie gibt, die die Quantenmechanik in einem größeren Kontext setzt und einige ihrer rätselhaften Eigenschaften erklärt, ähnlich wie die Quantenmechanik die klassische Mechanik in einen größeren Kontext gesetzt hat. Aber jede solche Theorie müsste immer noch mit der grundlegenden Zufälligkeit und Nichtlokalität der Quantenmechanik, wie sie durch das Bell-Theorem und verwandte Experimente bestätigt wurde, umgehen.

Es ist also durchaus möglich, dass wir eines Tages eine vollständigere Theorie der Physik haben werden, aber es ist unwahrscheinlich, dass diese Theorie die Rückkehr zu einer einfachen, lokal deterministischen Weltanschauung ermöglichen wird. Die Zufälligkeit und Nichtlokalität der Quantenmechanik scheinen fundamentale Aspekte unserer physischen Realität zu sein.

Trotz allem gibt es tatsächlich bereits einige theoretische Ansätze, die darauf abzielen, die Quantenmechanik in einen größeren Kontext zu setzen, der einige ihrer merkwürdigen Aspekte erklären könnte.

1. Bohm’sche Mechanik (auch bekannt als Pilot-Wellen-Theorie): Diese Interpretation schlägt vor, dass Teilchen tatsächlich gut definierte Positionen und Geschwindigkeiten haben, aber sie werden von einer „Pilotwelle“ geleitet, die durch die Wellenfunktion des Teilchens beschrieben wird. Die Pilotwelle ist global und nicht lokal, was bedeutet, dass sie eine sofortige Auswirkung auf große Entfernungen haben kann. Diese Interpretation ist deterministisch, aber sie ist mit der Relativitätstheorie schwer zu vereinbaren.
2. Viele-Welten-Interpretation: Diese Interpretation besagt, dass alle möglichen Ergebnisse einer quantenmechanischen Interaktion tatsächlich in unterschiedlichen „Welten“ oder „Universen“ auftreten. Sie eliminiert die Notwendigkeit des Wellenfunktionszusammenbruchs und könnte als deterministisch angesehen werden, wenn man das gesamte Multiversum betrachtet. Aber sie führt auch zu der seltsamen Vorstellung, dass sich das Universum ständig in eine enorme Anzahl von parallelen Realitäten aufspaltet.
3. Quantengravitation / Stringtheorie / Schleifenquantengravitation: Diese Ansätze versuchen, die Quantenmechanik mit der allgemeinen Relativitätstheorie zu vereinigen, um eine kohärente Theorie der Quantengravitation zu erstellen. Es wird oft spekuliert, dass eine vollständige Theorie der Quantengravitation einige der rätselhaften Aspekte der Quantenmechanik erklären könnte, aber bis jetzt haben wir noch keine solche Theorie.

Alle diese Ansätze haben interessante Aspekte und sie haben alle ihre eigenen Probleme und Schwierigkeiten. Keiner von ihnen wird allgemein als die „endgültige“ Interpretation der Quantenmechanik angesehen. Die Suche nach einem tieferen Verständnis der Quantenmechanik und ihrer Verbindung zum Rest der Physik ist immer noch ein sehr aktives Forschungsgebiet.

DIY Zufallsgenerator mit dem GDK-101 Modul

Unter der Annahme, dass der Zerfall eines Atoms ein wahrhaft zufälliges Ereignis darstellt, soll auf dieser Basis ein Zufallsgenerator entwickelt werden.

Die grundlegende Idee dabei besteht darin, das GDK-101 Modul einzusetzen, welches in der Lage ist, Gammastrahlung mittels Photodioden zu detektieren.

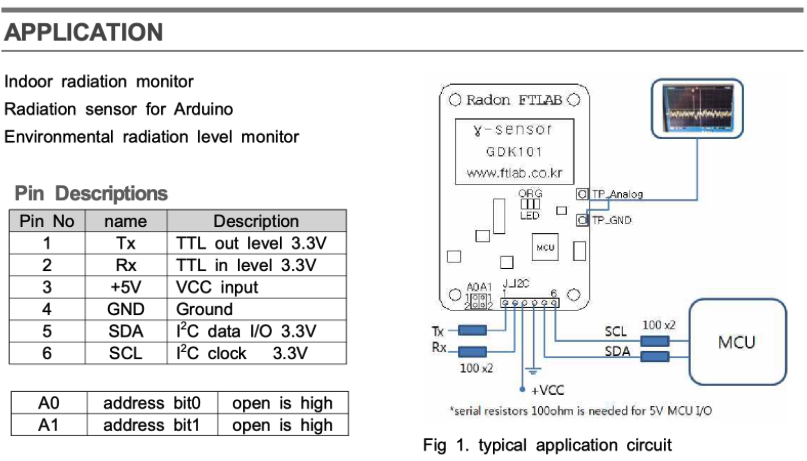
Die Aktivität kann über die I2C-Schnittstelle ausgelesen werden. Unser Ziel ist es jedoch, einzelne Ereignisse zu erfassen. Hierfür bietet das Modul die Anschlussmöglichkeit „TP_ANALOG, TP_GND“. Laut Blockdiagramm liegt dieser Anschluss noch vor der Signalverarbeitung, die schließlich zu einem Ereignis führt, das die MCU auf dem Board als solches bewertet. Leider lässt sich das Signal des Vibrationssensors nicht aufzeichnen.

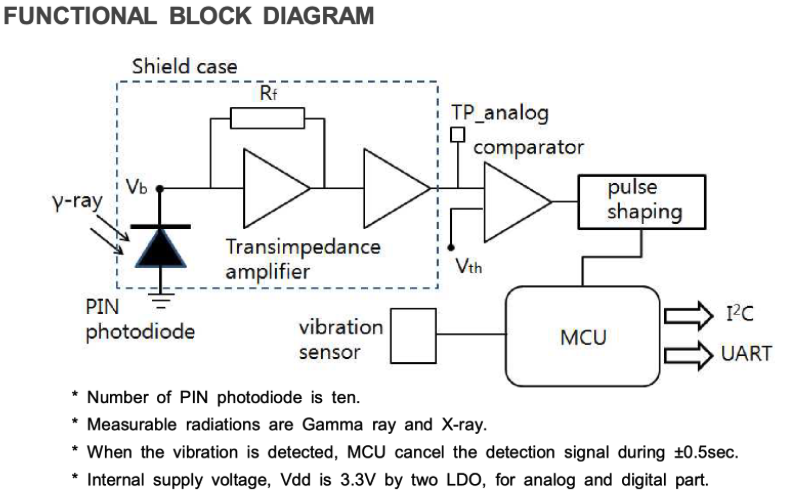
Daher müssen wir uns das eigentliche „TP_analog“-Signal genauer ansehen.

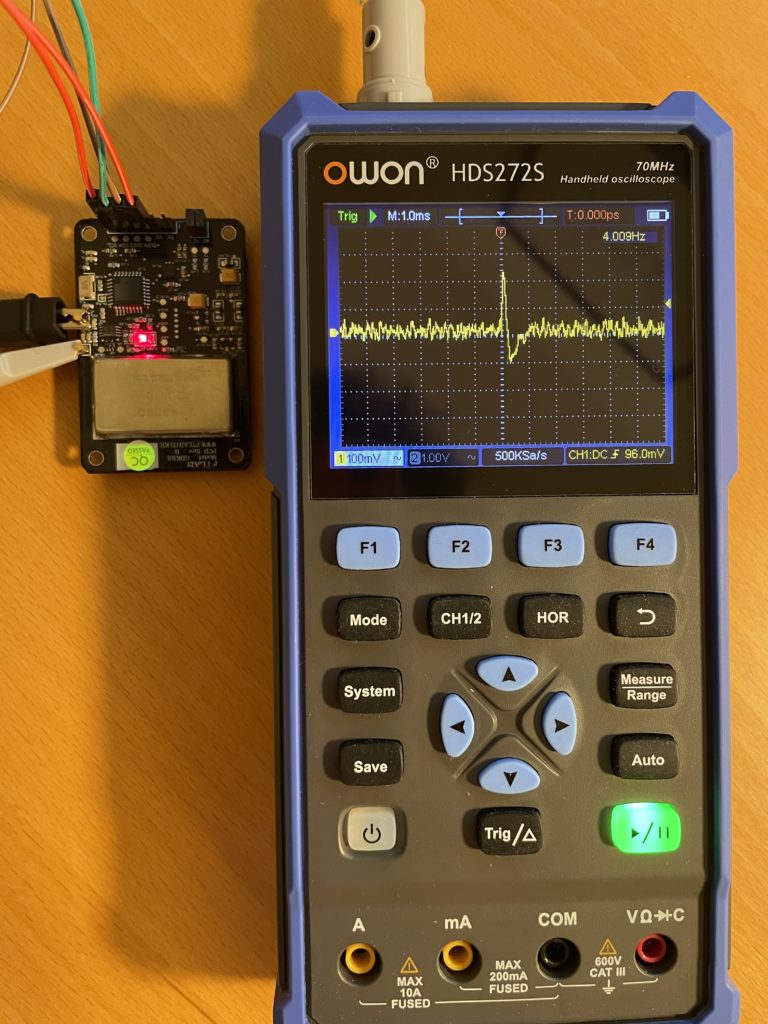
Es zeigt sich ein Grundrauschen und ein Signal-Peak, welcher auch von der MCU entsprechend interpretiert wird, wie die rote LED signalisiert.

Ein Blick in das Datenblatt verrät die Ausmaße des Grundrauschens („Base noise level of analog output“) und den Peak eines Ereignisses („Analog output peak“).

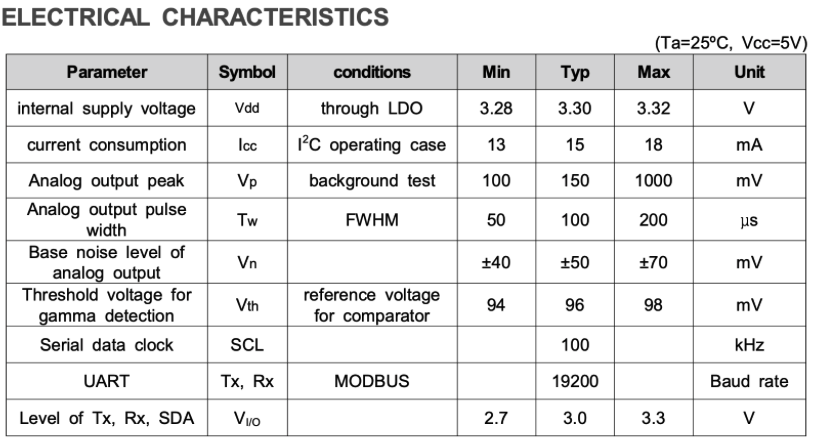
Mit diesem Wissen lässt sich eine erst Testkonstruktion mit einem Pi Pico erstellen.

	GDK-101	Pi Pico
Ground	GND	GND
VBUS=5V	5V	VBUS
Ground	TP_GND	GND
Signal	TP_ANALOG	GP26_A0

Ein kurzes Testscript in MicroPhyton für den Pi Pico

from machine import ADC
import utime as time

# Variables
voltage_adc = ADC(0)  # ADC channel
# The random Byte List
randomByte = []
# Up counting Number interrupted by Gamma-Event
randomNumberCounting = 0
# List for four Values of time differences
timeValues = []

start = time.ticks_us()

while True:
    # Read the ADC Value and convert it to voltage
    adc_voltage = voltage_adc.read_u16() * 3.3 / 65535

    #if len(voltagesWindowFrame) < windowFrameLength:
    #    voltagesWindowFrame.append(adc_voltage)
    #else:  
    #    voltagesWindowFrame = rotate(voltagesWindowFrame, 1)
    #    voltagesWindowFrame[windowFrameLength-1] = adc_voltage

    if adc_voltage > 0.13:
        print("Gamma-Event: "+str(adc_voltage))

        print("RandomNumberCounting:"+str(randomNumberCounting))
        # Write randomNumberCounting to file
        file = open ("rnumbers.txt", "a") 
        file.write(str(randomNumberCounting)+"\n")
        file.close()
        # due to upconting at the end -1
        randomNumberCounting = -1
        
        timediff = time.ticks_diff(time.ticks_us(), start)

        #Rbool 
        rbool = 0
        number = int(timediff)
        mod = number % 2
        #if number is odd it's a 'yes' otherwise 'no'
        if mod > 0:
            rbool = 1
      
        print("Rbool:"+str(rbool))

        if len(timeValues) < 3:
            timeValues.append(timediff)
        else:
            timeValues.append(timediff)
            print(timeValues)

            timeDiff1 = timeValues[1] - timeValues[0]
            timeDiff2 = timeValues[3] - timeValues[2]

            timeDiffRes = timeDiff1 - timeDiff2

            if len(randomByte) < 7:

                if timeDiffRes < 0:
                    randomByte.append(0)
                else:
                    randomByte.append(1)
                
                print("RByte:"+str(randomByte))
            else:
                if timeDiffRes < 0:
                    randomByte.append(0)
                else:
                    randomByte.append(1)

                #Convert randomByte to Integer
                randomNumber = int(''.join(map(str, randomByte)), 2)
                print("RByte ready:"+str(randomByte)+" : "+str(randomNumber))
                #Write Integer to File
                file = open ("rbytes.txt", "a")
                file.write(str(randomNumber)+"\n")
                file.close()

                #Clean randomByte for next
                randomByte = []

            #Clean timeValues for nex
            timeValues = []
        
        #Start new counter till next Gamma-Event
        start = time.ticks_us()
    
    if randomNumberCounting < 9:
        randomNumberCounting = randomNumberCounting + 1
    else:
        randomNumberCounting = 0

Ein erster Versuch

Gamma-Event: 0.1619409
RandomNumberCounting:3
Rbool:0
Gamma-Event: 0.1909453
RandomNumberCounting:3
Rbool:0
Gamma-Event: 0.277203
RandomNumberCounting:6
Rbool:1
Gamma-Event: 0.244976
RandomNumberCounting:5
Rbool:1
[7428448, 10645944, 7464333, 4101459]
RByte:[1]
Gamma-Event: 0.2602838
RandomNumberCounting:7
Rbool:0
Gamma-Event: 0.2087205
RandomNumberCounting:3
Rbool:0
Gamma-Event: 0.1740261
RandomNumberCounting:8
Rbool:0
Gamma-Event: 0.1627466
RandomNumberCounting:1
Rbool:0
[2744050, 64346, 932702, 2378432]
RByte:[1, 0]
Gamma-Event: 0.1514671
RandomNumberCounting:9
Rbool:0
Gamma-Event: 0.1321309
RandomNumberCounting:3
Rbool:0
Gamma-Event: 0.2111376
RandomNumberCounting:0
Rbool:0
Gamma-Event: 0.2433646
RandomNumberCounting:7
Rbool:0
[702138, 4624348, 11233966, 2028458]
RByte:[1, 0, 1]
Gamma-Event: 0.4158297
RandomNumberCounting:2
Rbool:1
Gamma-Event: 0.1458274
RandomNumberCounting:5
Rbool:1
Gamma-Event: 0.1675807
RandomNumberCounting:1
Rbool:1
Gamma-Event: 0.1450217
RandomNumberCounting:7
Rbool:0
[956581, 3620373, 3929931, 886802]
RByte:[1, 0, 1, 1]
Gamma-Event: 0.1788601
RandomNumberCounting:9
Rbool:0
Gamma-Event: 0.1877226
RandomNumberCounting:5
Rbool:1
Gamma-Event: 0.1313252
RandomNumberCounting:6
Rbool:1
Gamma-Event: 0.3182925
RandomNumberCounting:6
Rbool:0
[1085948, 10321711, 2677141, 1989832]
RByte:[1, 0, 1, 1, 1]
Gamma-Event: 0.1442161
RandomNumberCounting:5
Rbool:0
Gamma-Event: 0.2063035
RandomNumberCounting:0
Rbool:1
Gamma-Event: 0.1530785
RandomNumberCounting:2
Rbool:0
Gamma-Event: 0.2860654
RandomNumberCounting:0
Rbool:0
[3319512, 3371609, 2438458, 1587544]
RByte:[1, 0, 1, 1, 1, 1]
Gamma-Event: 0.1546898
RandomNumberCounting:3
Rbool:0
Gamma-Event: 0.1466331
RandomNumberCounting:6
Rbool:0
Gamma-Event: 0.2232227
RandomNumberCounting:6
Rbool:1
Gamma-Event: 0.1329366
RandomNumberCounting:1
Rbool:0
[9273310, 20332106, 7847499, 16967514]
RByte:[1, 0, 1, 1, 1, 1, 0]
Gamma-Event: 0.1651637
RandomNumberCounting:9
Rbool:0
Gamma-Event: 0.1828885
RandomNumberCounting:6
Rbool:1
Gamma-Event: 0.1377707
RandomNumberCounting:1
Rbool:0
Gamma-Event: 0.1426047
RandomNumberCounting:4
Rbool:1
[10405474, 1322747, 4329934, 8921667]
RByte ready:[1, 0, 1, 1, 1, 1, 0, 0] : 188

Wir haben wahrscheinlich unsere ersten Zufallszahlen generiert!

Als nächstes müssen wir überprüfen, ob es sich dabei wirklich um Zufall handelt. Das ist der Zeitpunkt für einen weiteren Beitrag.