Inhalt
Einführung
Deep Q-Networks (DQNs) repräsentieren eine weitreichende Entwicklung im Bereich des Reinforcement Learnings (RL). Sie stellen die Verschmelzung von klassischen Q-Learning-Algorithmen mit Deep Learning dar und bieten die Möglichkeit, komplexe Probleme zu lösen, die mit klassischen Methoden bisher nicht so einfach zu handhaben waren.
Klassische Methoden des Reinforcement Learning stoßen oft an Grenzen, wenn es um hochdimensionale Eingabedaten oder um komplexe Aufgabenstellungen geht. Ein Meilenstein wurde im Jahr 2013 erreicht, als Forscher von DeepMind ihre Arbeit zur Integration von Convolutional Neural Networks (CNNs) mit Q-Learning veröffentlichten. Sie demonstrierten, dass ihr Deep Q Network in der Lage war, eine Reihe von Atari-Spielen zu meistern, indem es direkt aus den Pixeln der Spielszenen lernte.
Das Labyrinth
Im Folgenden wollen wir das Prinzip der DQNs anhand eines einfachen Labyrinth Spieles herleiten welches aus 4×4 Feldern besteht.
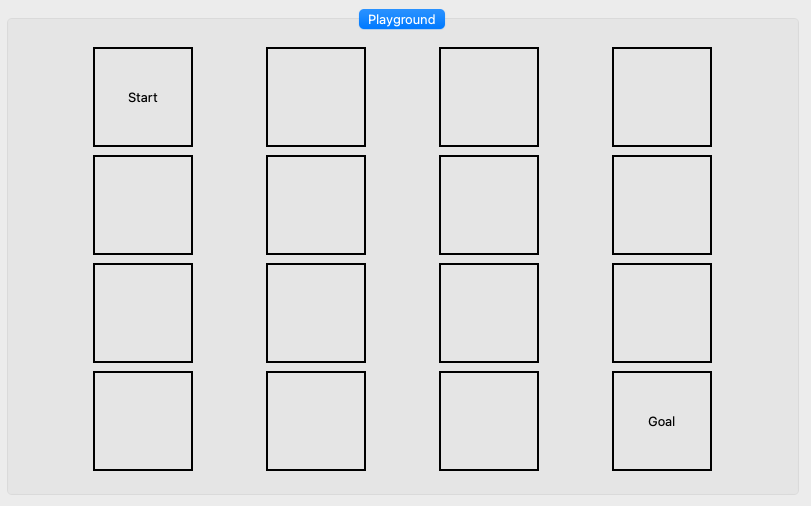
Der Start ist oben links und das Ziel unten rechts. Die Aufgabe für unsere Spielfigur (AGENT) wird es sein, den optimalen Weg zu finden.
Ziel ist es also ein Methode / einen Algorithmus zu finden, in welcher der Agent sich zunächst zufällig auf dem Spielfeld bewegt und mit der Zeit lernt, auf welchem Feld (Zustand ![]() ) er sie wie (Aktion
) er sie wie (Aktion ![]() ) bewegen muss, um möglichst schnell das Ziel zu erreichen.
) bewegen muss, um möglichst schnell das Ziel zu erreichen.
Hierzu betrachten wir zunächst das Q in DQN.
Q: Grundlagen des Q-Learning
Q-Learning ist ein Modell-freier Reinforcement-Learning-Algorithmus, der darauf abzielt, die optimale Strategie für einen Agenten (Figur in dem Labyrinth) in einer unbekannten Umgebung (Labyrinth) zu finden. In einem Markow-Entscheidungsprozess (MEP) lernt der Agent eine Funktion ( ![]() ), die den erwarteten langfristigen Nutzen oder die kumulative Belohnung angibt, wenn der Agent im Zustand (
), die den erwarteten langfristigen Nutzen oder die kumulative Belohnung angibt, wenn der Agent im Zustand ( ![]() ) die Aktion (
) die Aktion ( ![]() ) ausführt.
) ausführt.
Kurz gesagt haben wir einen Agenten der auf Grundlage eines Belohnungssystems agiert. Anfangs führt der Agent zufällig gewählte Handlungen aus, die anschließend bewertet werden. Er lernt aus diesen Bewertungen und passt sein zukünftiges Verhalten an. Da er alle möglichen Szenarien erkunden muss, um optimal handeln zu können, kann der Lernprozess zeitaufwendig sein.
Zur Entscheidungsfindung wird eine sogenannte Q-Matrix erstellt und im Verlauf immer wieder angepasst. Man kann sich diese Matrix als eine Tabelle vorstellen, in der die Zeilen für verschiedene Situationen und die Spalten für mögliche Handlungen stehen.
| Zustand | Hoch | Runter | Links | Rechts |
|---|---|---|---|---|
| 0 | 0.1 | 0.2 | -1 | 0.2 |
| 1 | -1 | 0.1 | 0.1 | -1 |
| 2 | … | … | … | … |
| 4 | 0.3 | 0.1 | 0.2 | -1 |
| 8 | 0.4 | 0.1 | 0.3 | 0.5 |
| 12 | -1 | 0.6 | -1 | 0.5 |
In dieser Tabelle werden Q-Werte gespeichert, die den Wert einer bestimmten Handlung in einer spezifischen Situation repräsentieren. Wenn der Agent eine Entscheidung treffen muss, schaut er in dieser Q-Matrix nach der Handlung mit dem höchsten Q-Wert für seine aktuelle Situation.
Wie sieht das in einem Beispiel aus? Hierzu müssen wir uns zunächst anschauen, wie die Belohnung (bzw. der Q-Wert) berechnet werden.
Q-Wert-Update
Das Herzstück des Q-Learning-Algorithmus ist die Aktualisierung der Q-Werte für die Q-Matrix. Diese Aktualisierung erfolgt in der Regel über die Q-Learning-Update-Gleichung:
![]()
Hier ist:
- (
 ) der aktuelle Zustand
) der aktuelle Zustand - (
 ) die ausgewählte Aktion
) die ausgewählte Aktion - (
 ) die erhaltene Belohnung
) die erhaltene Belohnung - (
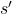 ) der nächste Zustand
) der nächste Zustand - (
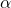 ) die Lernrate (zwischen 0 und 1)
) die Lernrate (zwischen 0 und 1) - (
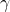 ) der Diskontfaktor (zwischen 0 und 1)
) der Diskontfaktor (zwischen 0 und 1) - (
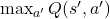 ) der höchste Q-Wert für den nächsten Zustand ( s‘ )
) der höchste Q-Wert für den nächsten Zustand ( s‘ )
Einschub: Wie man zur Q-Wert-Update Funktion gelangt
Für ein besseres Verständnis der Vorgänge hier der Versuch die Idee hinter der Funktion zu erklären.
Das Ziel: Die erwartete Rendite finden
Das allgemeine Ziel besteht darin, eine bestimmte Form der kumulativen Belohnung, oft als „Rendite“ (return) bezeichnet, zu maximieren. Ein einzelner Verlauf (trajectory) des Agenten durch die Umgebung kann durch eine Sequenz von Zuständen, Aktionen und Belohnungen dargestellt werden: (![]() ).
).
Die Rendite ( ![]() ) zu einem Zeitpunkt (
) zu einem Zeitpunkt ( ![]() ) ist die Summe der zukünftigen Belohnungen, die der Agent erhalten wird, wobei jede Belohnung durch einen Faktor (
) ist die Summe der zukünftigen Belohnungen, die der Agent erhalten wird, wobei jede Belohnung durch einen Faktor ( ![]() ) diskontiert wird. Mathematisch wird die Rendite (
) diskontiert wird. Mathematisch wird die Rendite ( ![]() ) als
) als
![Rendered by QuickLaTeX.com \[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots = \sum_{k=0}^\infty \gamma^k R_{t+k+1}\]](https://atlane.de/wp-content/ql-cache/quicklatex.com-bc847d52c4e9048ba7753fbdfbcfe97d_l3.png)
definiert. Hierbei ist ( ![]() ) der Diskontierungsfaktor (discount factor), der von
) der Diskontierungsfaktor (discount factor), der von ![]() bis
bis ![]() variiert. Dieser Faktor modelliert die Idee, dass zukünftige Belohnungen weniger wertvoll sind als unmittelbare Belohnungen. (
variiert. Dieser Faktor modelliert die Idee, dass zukünftige Belohnungen weniger wertvoll sind als unmittelbare Belohnungen. ( ![]() ) ist die Belohnung, die zum Zeitpunkt (
) ist die Belohnung, die zum Zeitpunkt ( ![]() ) erhalten wird.
) erhalten wird.
Q-Funktion-Definition
Die ( ![]() )-Funktion ist als die erwartete Rendite für die Ausführung der Aktion (
)-Funktion ist als die erwartete Rendite für die Ausführung der Aktion ( ![]() ) im Zustand (
) im Zustand ( ![]() ) definiert und folgt anschließend einer bestimmten Strategie (genannt Policy) (
) definiert und folgt anschließend einer bestimmten Strategie (genannt Policy) ( ![]() ):
):
![]()
Wenn wir die Formel für ( ![]() ) in diese Definition einsetzen, erhalten wir:
) in diese Definition einsetzen, erhalten wir:
![]()
Diese Formel ist aber noch nicht unsere von oben?
In unserem Fall des Q-Learning ist ![]() die Belohnung zur Zeit
die Belohnung zur Zeit ![]() und
und ![]() ist der Diskontierungsfaktor.
ist der Diskontierungsfaktor.
Die Idee besteht darin, ![]() zu schätzen, indem man die unmittelbare Belohnung
zu schätzen, indem man die unmittelbare Belohnung ![]() sowie die diskontierten zukünftigen Belohnungen betrachtet. Die wertvollste Aktion
sowie die diskontierten zukünftigen Belohnungen betrachtet. Die wertvollste Aktion ![]() im nächsten Zustand
im nächsten Zustand ![]() ist gegeben durch
ist gegeben durch ![]() . Das können wir so schreiben:
. Das können wir so schreiben:
![]()
Hier kommt ![]() , die Lernrate, ins Spiel. Die Aktualisierungsregel kombiniert die aktuelle und neue Schätzung:
, die Lernrate, ins Spiel. Die Aktualisierungsregel kombiniert die aktuelle und neue Schätzung:
![]()
(Die Formel von oben!)
Für das spätere Deep-Q-Network learning brauchen wir noch Umformungen.
Wenn man dies ausklammert, erhält man:
![]()
Nach Vereinfachung erhalten wir:
![Rendered by QuickLaTeX.com \[Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( \underbrace{r_t + \gamma \max_{a'} Q(s_{t+1}, a')}_{\text{Temporal Difference Factor}} - Q(s_t, a_t) \right)\]](https://atlane.de/wp-content/ql-cache/quicklatex.com-539c4577431c1e7c7a154eb9341a6485_l3.png)
Und da haben wir die Aktualisierungsformel für Q-Lernen!
Für was das Umstellen und die Definition des Temporal Difference Factor ?
Dieser Term stellt den geschätzten Wert dar, wenn man die Aktion ( ![]() ) im Zustand (
) im Zustand ( ![]() ) ausführt und danach optimal handelt. Er kombiniert die unmittelbare Belohnung (
) ausführt und danach optimal handelt. Er kombiniert die unmittelbare Belohnung ( ![]() ), die man erhält, nachdem man die Aktion (
), die man erhält, nachdem man die Aktion ( ![]() ) im Zustand (
) im Zustand ( ![]() ) ausgeführt hat, mit dem diskontierten geschätzten Wert der bestmöglichen nächsten Aktion (
) ausgeführt hat, mit dem diskontierten geschätzten Wert der bestmöglichen nächsten Aktion ( ![]() ).
).
Hier eine Aufschlüsselung:
- (
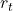 ) ist die unmittelbare Belohnung, die man erhält, nachdem man die Aktion (
) ist die unmittelbare Belohnung, die man erhält, nachdem man die Aktion ( 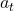 ) im Zustand (
) im Zustand ( 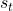 ) ausgeführt hat.
) ausgeführt hat. - (
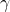 ) ist der Diskontierungsfaktor, der den Wert zukünftiger Belohnungen herunterskaliert. Es ist eine Zahl zwischen 0 und 1. Ein Wert nahe 0 macht den Agenten kurzfristig orientiert, der hauptsächlich auf unmittelbare Belohnungen achtet, während ein Wert nahe 1 den Agenten langfristig orientiert macht und mehr Wert auf langfristige Belohnungen legt.
) ist der Diskontierungsfaktor, der den Wert zukünftiger Belohnungen herunterskaliert. Es ist eine Zahl zwischen 0 und 1. Ein Wert nahe 0 macht den Agenten kurzfristig orientiert, der hauptsächlich auf unmittelbare Belohnungen achtet, während ein Wert nahe 1 den Agenten langfristig orientiert macht und mehr Wert auf langfristige Belohnungen legt. - (
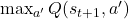 ) ist die maximale erwartete zukünftige Belohnung, wenn man sich im nächsten Zustand (
) ist die maximale erwartete zukünftige Belohnung, wenn man sich im nächsten Zustand ( 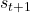 ) befindet und davon ausgeht, dass man die bestmögliche Aktion von diesem Zustand aus wählt.
) befindet und davon ausgeht, dass man die bestmögliche Aktion von diesem Zustand aus wählt.
Zusammengefasst dient ( ![]() ) als Zielwert in der Q-Learning-Aktualisierungsformel. Dieser Zielwert repräsentiert, was der Agent als optimalen erwarteten kumulativen Wert für das aktuelle Zustands-Aktions-Paar (
) als Zielwert in der Q-Learning-Aktualisierungsformel. Dieser Zielwert repräsentiert, was der Agent als optimalen erwarteten kumulativen Wert für das aktuelle Zustands-Aktions-Paar ( ![]() ) ansieht, unter Berücksichtigung sowohl unmittelbarer als auch zukünftiger Belohnungen.
) ansieht, unter Berücksichtigung sowohl unmittelbarer als auch zukünftiger Belohnungen.
Der Q-Learning-Algorithmus verwendet dann diesen Zielwert, um den aktuellen geschätzten Wert ( ![]() ) in eine Richtung zu aktualisieren, die den Unterschied zwischen dem geschätzten Wert und dem Zielwert minimiert. Dieser „Unterschied“ ist im Wesentlichen eine Form von Fehler, den der Algorithmus zu minimieren versucht, während er aus immer mehr Erfahrungen lernt.
) in eine Richtung zu aktualisieren, die den Unterschied zwischen dem geschätzten Wert und dem Zielwert minimiert. Dieser „Unterschied“ ist im Wesentlichen eine Form von Fehler, den der Algorithmus zu minimieren versucht, während er aus immer mehr Erfahrungen lernt.
Dies ist wichtig, da wir später hierfür verschiedene neuronale Netzwerke verwenden werden.
Interpretation der Q-Funktion:
- (
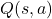 ) sagt aus, was die erwartete Rendite ist, wenn Sie die Aktion (
) sagt aus, was die erwartete Rendite ist, wenn Sie die Aktion (  ) im Zustand (
) im Zustand (  ) ausführen und anschließend optimal handeln (oder einer spezifischen Strategie (Policy) (
) ausführen und anschließend optimal handeln (oder einer spezifischen Strategie (Policy) ( 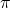 ) folgen).
) folgen). - (
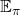 ) bezeichnet den Erwartungswert unter der Strategie (
) bezeichnet den Erwartungswert unter der Strategie ( 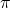 ). Das bedeutet, dass der Erwartungswert unter der Annahme berechnet wird, dass der Agent der Strategie (
). Das bedeutet, dass der Erwartungswert unter der Annahme berechnet wird, dass der Agent der Strategie ( 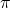 ) folgt, nachdem er die Aktion (
) folgt, nachdem er die Aktion (  ) im Zustand (
) im Zustand (  ) ausgeführt hat.
) ausgeführt hat. - (
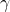 ) ist der Abzinsungsfaktor (discount factor). Es ist eine Zahl zwischen 0 und 1, die die Berücksichtigung des Agenten für zukünftige Belohnungen modelliert. Ein hoher (
) ist der Abzinsungsfaktor (discount factor). Es ist eine Zahl zwischen 0 und 1, die die Berücksichtigung des Agenten für zukünftige Belohnungen modelliert. Ein hoher ( 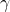 ) bedeutet, dass der Agent zukünftige Belohnungen im Verhältnis zu unmittelbaren Belohnungen hoch bewertet.
) bedeutet, dass der Agent zukünftige Belohnungen im Verhältnis zu unmittelbaren Belohnungen hoch bewertet. - (
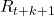 ) ist die Belohnung, die zum Zeitpunkt (
) ist die Belohnung, die zum Zeitpunkt ( 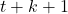 ) erhalten wird. Es ist das, was der Agent erhält, nachdem er (
) erhalten wird. Es ist das, was der Agent erhält, nachdem er ( 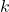 ) Übergänge vom aktuellen Zustand (
) Übergänge vom aktuellen Zustand (  ) gemacht hat, wenn die Aktion (
) gemacht hat, wenn die Aktion (  ) zum Zeitpunkt (
) zum Zeitpunkt ( 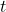 ) ausgeführt wurde.
) ausgeführt wurde. - (
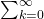 ) bedeutet, dass wir die kumulative Belohnung betrachten, die von (
) bedeutet, dass wir die kumulative Belohnung betrachten, die von ( 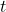 ) beginnt und in die Zukunft geht.
) beginnt und in die Zukunft geht.
Somit fasst die Formel die Idee des „Wertes“ des Ausführens einer bestimmten Aktion ( ![]() ) in einem bestimmten Zustand (
) in einem bestimmten Zustand ( ![]() ) unter einer bestimmten Strategie (
) unter einer bestimmten Strategie ( ![]() ) zusammen.
) zusammen.
Beispiel: Das Labyrinth-Spiel
Nehmen wir als Beispiel unser 4×4 Labyrinth, in dem ein Agent von der oberen linken Ecke (Start) zur unteren rechten Ecke (Ziel) gelangen soll. Der Agent erhält eine Belohnung von +1, ansonsten eine Strafe on -0.1.
S 0 0 0
0 0 0 0
0 0 0 0
0 0 0 G- S = Start
- G = Ziel
- 0 = Freies Feld
Die möglichen Aktionen sind Hoch, Runter, Links und Rechts. Zuerst initialisieren wir die Q-Tabelle mit Nullen für jeden Zustand-Aktions-Paar. Dann folgt der Agent einer Strategie (z.B. epsilon-greedy), um Aktionen auszuwählen und die Q-Werte zu aktualisieren, während er sich durch das Labyrinth bewegt.
Für die Zustandsaktualisierung verwenden wir die oben genannte Q-Learning-Update-Gleichung. Nehmen wir an, der Agent befindet sich im Startzustand und entscheidet sich, nach rechts zu gehen. Er landet in einem freien Feld und erhält eine Belohnung von 0. Wenn wir ( ![]() ) und (
) und ( ![]() ) setzen, wird der neue Q-Wert für das Paar (Start, Rechts) aktualisiert als:
) setzen, wird der neue Q-Wert für das Paar (Start, Rechts) aktualisiert als:
![]()
Da die Q-Werte für die angrenzenden Zustände noch bei Null sind, bleibt der Q-Wert unverändert. Mit der Zeit konvergiert diese Methode jedoch zur optimalen Strategie, wenn der Agent genug Erfahrung gesammelt hat.
Die Q-Tabelle
In unserem 4×4 Labyrinth-Beispiel könnten die Q-Wert-Tabelle wie folgt dargestellt werden um die erwartete Rendite für jede Aktion in jedem Zustand zu speichern. Angenommen, wir nummerieren die Zustände von 0 bis 15, beginnend mit der oberen linken Ecke und von links nach rechts, von oben nach unten. Wir haben 4 mögliche Aktionen: Hoch (0), Runter (1), Links (2) und Rechts (3).
Die Q-Wert-Matrix könnte wie folgt aussehen (die Werte sind hypothetisch und dienen nur der Veranschaulichung):
| Zustand | Hoch | Runter | Links | Rechts |
|---|---|---|---|---|
| 0 | 0.1 | 0.2 | -1 | 0.2 |
| 1 | -1 | 0.1 | 0.1 | -1 |
| 2 | … | … | … | … |
| 4 | 0.3 | 0.1 | 0.2 | -1 |
| 8 | 0.4 | 0.1 | 0.3 | 0.5 |
| 12 | -1 | 0.6 | -1 | 0.5 |
In dieser Tabelle zeigt jede Zeile die Q-Werte für die 4 möglichen Aktionen in einem bestimmten Zustand an. Zum Beispiel:
- Für den Zustand 0 (Startpunkt):
- Hoch gehen hat einen Q-Wert von 0.1
- Runter gehen hat einen Q-Wert von 0.2
- Links gehen hat einen Q-Wert von -1 (vielleicht weil es nicht möglich ist)
- Rechts gehen hat einen Q-Wert von 0.2
- Für den Zustand 4:
- Hoch gehen hat einen Q-Wert von 0.3
- Runter gehen hat einen Q-Wert von 0.1
- Links gehen hat einen Q-Wert von 0.2
- Rechts gehen hat einen Q-Wert von -1 (vielleicht weil es eine Blockade gibt)
Die Q-Werte werden durch den Q-Learning-Prozess aktualisiert. Sie fangen normalerweise bei Null an und werden im Laufe der Zeit durch die Interaktion des Agenten mit der Umgebung besser. Ein gut trainierter Agent würde hohe Q-Werte für Aktionen haben, die ihn dem Ziel näher bringen, und niedrige oder negative Q-Werte für Aktionen, die ihn entweder von dem Ziel wegbewegen oder in einen unerwünschten Zustand wie eine Blockade bringen.
Am Ende hat unser Agent also eine Art Anweisungstabelle in welcher er Nachschauen kann, welche Aktion am meisten Sinn macht, je nachdem wo er gerade auf den Feldern steht.
Q-Learning ist ein einfaches Verfahren im Reinforcement Learning für das Lernen von optimalen Strategien in unbekannten Umgebungen. Für was brauchen wir dann das Deep in DQN?
DQN: Q-Learning trifft Deep Learning
In der Praxis erweist sich die Verwendung einer Q-Tabelle für große und kontinuierliche Zustands- und Aktionsräume als wenig praktikabel. Dies ist besonders bei komplexen Aufgaben wie dem autonomen Fahren der Fall. Hier kommen Deep Q-Networks (DQNs) ins Spiel. Sie kombinieren das Konzept des Q-Learnings mit neuronalen Netzwerken. Ein zentrales Element ist das Q-Network, das zur Approximation der Q-Wert-Funktion dient und die traditionelle Q-Tabelle ersetzt. Statt in einer Tabelle nachzuschlagen, welche Q-Werte einer Aktion in einem bestimmten Zustand zugeordnet sind, konsultiert man das neuronale Netzwerk, das einen approximierten Wert zurückgibt. Das Ziel besteht darin, das Netzwerk so zu trainieren, dass es den Q-Wert einer Abfrage möglichst genau bestimmen kann.
Komponenten: Was wir hierfür brauchen
Einige Komponenten kennen wir bereits, sollen aber nochmals wiederholt werden um den Überblick zu behalten.
- Umwelt: Die Welt, in der der Agent Handlungen ausführt und Belohnungen erhält. In unserem Beispiel das 4×4 Labyrinth.
- Agent: Die Entität, die aus Handlungen und Belohnungen lernt. Unser Agent der sich durch das Labyrinth bewegt
- Zustand: Ein Schnappschuss der Umwelt zu einem bestimmten Zeitpunkt. In unserem Beispiel der Ort an welchem sich unser Agent aufhält.
- Aktion: Ein Zug, den der Agent in der Umwelt macht. Die 4-möglichen Richtungen (wenn möglich)
- Belohnung: Ein Wert, den der Agent nach der Ausführung einer Aktion erhält.
- Q-Funktion: haben wir oben ausführlich besprochen
- NEU ! Neuronale Netzwerke: werden verwendet, um die Q-Funktion zu approximieren. Die Besonderheit, wir brauchen hier zwei Netzwerke!
Wir verwenden also keine Q-Tabelle mehr in welcher wir die Q-Werte abspeichern sondern trainieren ein neuronales Netzwerk darauf, dass es uns Q-Werte für spezifische Zustände vorhersagt.
Deep Q-Networks (DQN)
Ein Deep Q-Network (DQN) verwendet zwei separate Netzwerke, um die Stabilität und die Konvergenze der Lernalgorithmen zu verbessern. Diese zwei Netzwerke werden oft als „Zielnetzwerk“ (target network) und „Hauptnetzwerk“ (main network oder policy network) bezeichnet.
- Q-Network: Dies ist das Hauptnetzwerk, das der Agent verwendet, um zu entscheiden, welche Aktionen er ausführen soll. Es nimmt den aktuellen Zustand als Eingabe und gibt Q-Werte für jede mögliche Aktion aus. Die Q-Werte repräsentieren die erwartete Rendite (kumulierte abgezinste zukünftige Belohnungen) des Ausführens jeder Aktion im aktuellen Zustand und dann des Folgens der aktuellen Richtlinie danach. Das Q-Network wird häufig aktualisiert, um den Unterschied zwischen seinen Vorhersagen und den Q-Zielen zu minimieren.
- Target Network: Die Berechnung der Ziel-Q-Werte (also der besten geschätzten zukünftigen Belohnungen) ist ein wichtiger Schritt im Trainingsprozess. In einem Standard-Q-Learning-Ansatz würde man die aktuellen Gewichtungen des Q-Netzwerks selbst verwenden, um diese Ziel-Q-Werte zu berechnen. Dies kann jedoch zu instabilen oder divergierenden Training führen, da die Q-Werte ständig aktualisiert werden. Das Ziel-Netzwerk hilft, dieses Problem zu lösen. Seine Gewichtungen werden weniger häufig aktualisiert (z.B. alle N Schritte oder alle N Episoden) und bleiben in der Zwischenzeit konstant. Diese stabilen Ziel-Q-Werte ermöglichen ein effektiveres und stabileres Training des Q-Netzwerks.
Einschub: Warum sind zwei Netzwerke notwendig?
- Stabilität: Durch die Verwendung eines Zielnetzwerks, das seltener aktualisiert wird, erhält man eine stabilere Schätzung der Zielfunktionswerte. Dies hilft, die Oszillationen im Lernprozess zu verringern.
- Konvergenz: Die Verwendung von zwei Netzwerken hilft dem DQN-Algorithmus, schneller und zuverlässiger zu konvergieren. Wenn das Hauptnetzwerk und das Zielnetzwerk identisch und ständig aktualisiert würden, könnten die Q-Werte beginnen, in eine unerwünschte Richtung zu divergieren, was das Lernen erschwert.
- Entkopplung von Abhängigkeiten: Im Q-Learning wird die Q-Funktion sowohl für die Auswahl der Aktion (durch das Hauptnetzwerk) als auch für die Schätzung des zukünftigen Wertes (durch das Zielnetzwerk) verwendet. Diese doppelte Verwendung kann zu einer problematischen Korrelation führen. Durch die Verwendung von zwei separaten Netzwerken wird dieses Problem teilweise mitigiert.
Insgesamt verbessert die Verwendung von zwei Netzwerken in DQN die Robustheit und Leistung des Reinforcement Learning-Prozesses.
Wie lernt nun ein DQN? Der Trainingsprozess
- Initialisierung: Initialisiere das Q-Network mit zufälligen Gewichten. Kopiere diese Anfangsgewichte in das Target Network.
- Aktionsauswahl: Die Aktionsauswahl ist nicht unbedingt trivial. Wir müssen uns im Verlauf immer wieder entscheiden ob wir die Richtung aufgrund unseres Vorwissens oder explorativ wählen. Je mehr Erfahrung wir sammeln desto mehr sollten wir uns auf die Q-Werte verlassen, gleichzeitig dürfen wir aber nicht zu früh die zufällige explorative Wahl verlassen, da wir ja vielleicht noch andere Wege finden könnten, welche schlussendlich effektiver sind. Hierfür gibt es unterschiedliche Methoden.
Beispiel.:
Wähle ( ) aus (
) aus (  ) mit einer Epsilon-greedy Strategie:
) mit einer Epsilon-greedy Strategie:![Rendered by QuickLaTeX.com \[a =\begin{cases}\text{argmax}_{a} Q(s, a; \theta) & \text{mit Wahrscheinlichkeit } 1-\epsilon \\\text{zufällige Aktion} & \text{mit Wahrscheinlichkeit } \epsilon\end{cases}\]](https://atlane.de/wp-content/ql-cache/quicklatex.com-d44555e07f71caa834b41f2ef2088be8_l3.png)
- Aktion ausführen: Führe die ausgewählte Aktion in der Umgebung aus, wechsle zu einem neuen Zustand (
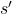 ) und erhalte eine Belohnung (
) und erhalte eine Belohnung (  ).
). - Erfahrung speichern: Speichere das Tupel (
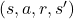 ) in einem Replay Buffer.
) in einem Replay Buffer. - Mini-Batch: Wähle zufällig einen Mini-Batch von Erfahrungen aus dem Replay Buffer.
- Q-Ziel berechnen: Verwende für jede Erfahrung im Mini-Batch das Target Network, um das Q-Ziel mit der Formel zu berechnen:
![Rendered by QuickLaTeX.com \[\text{Q-Target} = r + \gamma \max_{a'} Q(s', a'; \theta^-)\]](https://atlane.de/wp-content/ql-cache/quicklatex.com-78eeb8ce4bef35f34bac10ef920c0b53_l3.png)
wobei (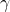 ) der Diskontierungsfaktor und (
) der Diskontierungsfaktor und ( 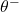 ) die Gewichte des Target Networks sind.
) die Gewichte des Target Networks sind.
- Q-Network aktualisieren: Verwende die Q-Ziele und das Q-Network, um den Verlust zu berechnen und einen Gradientenabstiegsschritt durchzuführen, um die Gewichte (
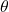 ) des Q-Networks zu aktualisieren.
) des Q-Networks zu aktualisieren.
![]()
- Target Network aktualisieren: Aktualisiere alle (
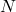 ) Schritte das Target Network, indem die Gewichte vom Q-Network kopiert werden (
) Schritte das Target Network, indem die Gewichte vom Q-Network kopiert werden ( 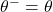 ).
).
Geht es auch etwas genauer?
Umgebung
- Zustände ( s ): 16 Zustände, die jeweils einer Zelle in einem 4×4-Gitter entsprechen (bezeichnet als (0) bis (15))
- Aktionen ( a ): 4 Aktionen: Hoch, Runter, Links, Rechts
- Belohnung ( r ): ( +1 ) für das Erreichen des Zielzustands, ( -0.1 ) ansonsten
Nehmen wir an, der Zielzustand befindet sich in der Zelle (15) (untere rechte Ecke).
Schritte
- Initialisiere Q-Netzwerk und Target-Netzwerk
Wir initialisieren ein neuronales Netzwerk (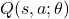 ) mit den Parametern (
) mit den Parametern ( 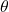 ) und ein Target-Netzwerk (
) und ein Target-Netzwerk ( 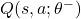 ) mit den Parametern (
) mit den Parametern ( 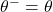 ).
).
- Initialisiere Replay Memory ( D )
Initialisiere ein Replay Memory (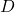 ), um Übergangstupel (
), um Übergangstupel ( 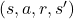 ) zu speichern.
) zu speichern.
- Trainings-Schleife
Für jede Episode in der Trainingsschleife:
- Initialisiere den Zustand (
 )
)
Beginne bei einem beliebigen Anfangszustand. - Wähle eine Aktion (
 )
)
Wähle ( ) aus (
) aus (  ) mit einer Epsilon-greedy Strategie:
) mit einer Epsilon-greedy Strategie:![Rendered by QuickLaTeX.com \[a =\begin{cases}\text{argmax}_{a} Q(s, a; \theta) & \text{mit Wahrscheinlichkeit } 1-\epsilon \\\text{zufällige Aktion} & \text{mit Wahrscheinlichkeit } \epsilon\end{cases}\]](https://atlane.de/wp-content/ql-cache/quicklatex.com-d44555e07f71caa834b41f2ef2088be8_l3.png)
- Führe Aktion ( a ) aus
- Beobachte die Belohnung (
 ) und den neuen Zustand (
) und den neuen Zustand ( 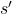 )
) - Speichere den Übergang
Speichere (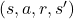 ) in (
) in (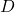 ).
). - Wähle eine zufällige Stichprobe aus (
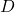 )
) - Wähle (
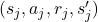 ) aus (
) aus (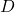 )
) - Berechne das Q-Learning-Ziel
Verwende das Target-Netzwerk, um den Ziel-Q-Wert für jeden ausgewählten Übergang zu berechnen:![Rendered by QuickLaTeX.com \[\text{Q-Target} = r_j + \gamma \max_{a'} Q(s_j', a'; \theta^-)\]](https://atlane.de/wp-content/ql-cache/quicklatex.com-768cae5f7c2f29c50406dcca484346c3_l3.png)
- Aktualisiere das Q-Netzwerk
Dies ist ein essentieller Schritt, da wir hier dem Netzwerk durch das zuvor berechnete Q-Learning-Ziel sagen können ob es eine gute oder schlechte Vorhersage gemacht hat und daran lernen kann.
Angenommen, wir befinden uns im Zustand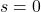 und haben die Aktion „Rechts“ ausgeführt, um in den Zustand
und haben die Aktion „Rechts“ ausgeführt, um in den Zustand 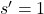 zu gelangen. Der erhaltene Reward
zu gelangen. Der erhaltene Reward  ist
ist 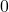 , und wir berechnen das Q-Target:
, und wir berechnen das Q-Target:
Die Loss-Funktion für diesen Übergang wird dann wie folgt sein:![Rendered by QuickLaTeX.com \[ \text{Q-Target} = 0 + 0.99 \times \max(Q(1, a; \theta^-)) \]](https://atlane.de/wp-content/ql-cache/quicklatex.com-93821492c2943e272f8807bf9986d8aa_l3.png)
Wir verwenden diesen Loss, um die Gewichtungen![Rendered by QuickLaTeX.com \[ \text{Loss} = \left( \text{Q-Target} - Q(0, \text{"Rechts"}; \theta) \right)^2 \]](https://atlane.de/wp-content/ql-cache/quicklatex.com-fe9b90c2b06884ec5edb36019c2e2157_l3.png)
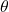 des Q-Netzwerks durch Gradientenabstieg zu aktualisieren. Der Gradient des Loss wird berechnet und benutzt, um die Gewichtungen in die Richtung zu bewegen, die den Loss minimiert:
des Q-Netzwerks durch Gradientenabstieg zu aktualisieren. Der Gradient des Loss wird berechnet und benutzt, um die Gewichtungen in die Richtung zu bewegen, die den Loss minimiert:
Dieser Schritt ist entscheidend für das Training des Netzwerks. Durch die Minimierung dieses Loss-Werts wird das Netzwerk besser darin, die Q-Werte korrekt zu approximieren, was wiederum ermöglicht, eine effiziente Politik (d.h. eine Sequenz von Aktionen) zu finden, um vom Startzustand zum Zielzustand zu gelangen.![Rendered by QuickLaTeX.com \[ \nabla_\theta \text{Loss} = -2 \left( \text{Q-Target} - Q(s, a; \theta) \right) \nabla_\theta Q(s, a; \theta) \]](https://atlane.de/wp-content/ql-cache/quicklatex.com-71b9ecb2440f332743d7e18abcd575a1_l3.png)
- Aktualisiere das Target-Netzwerk
Alle (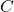 ) Schritte setze (
) Schritte setze ( 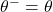 )
) - Schleife
( )
) - Beende, wenn der Zielzustand erreicht ist
Beispiel 4×4 Gitter:
- Initialisiere Zustand (
 )
)
- Beginne bei der Zelle (0).
- Wähle eine Aktion (
 )
)
- Mit (
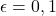 ) wähle entweder eine zufällige Aktion oder die Aktion, die (
) wähle entweder eine zufällige Aktion oder die Aktion, die ( 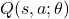 ) maximiert.
) maximiert.
- Mit (
- Führe Aktion (
 ) aus
) aus
- Bewege dich nach rechts zur Zelle (1).
- Speichere Übergang
- (
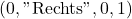 )
)
- (
- Stichprobe aus (
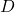 )
)
- Angenommen, wir wählen den gleichen Übergang (
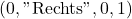 ).
).
- Angenommen, wir wählen den gleichen Übergang (
- Berechne Q-Learning-Ziel
- (
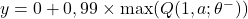 )
)
- (
- Aktualisiere Q-Netzwerk
- Aktualisiere (
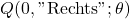 ) mit (
) mit ( 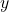 ).
).
- Aktualisiere (
- Aktualisiere Target-Netzwerk
- Angenommen, (
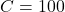 ), und wir aktualisieren (
), und wir aktualisieren ( 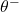 ) nach 100 Schritten.
) nach 100 Schritten.
- Angenommen, (
- Schleife
- (
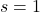 )
)
- (
Durch wiederholtes Anwenden dieser Schritte lernt das DQN, durch das 4×4-Gitter zu navigieren, um das Ziel in der Zelle (15) zu erreichen.
Hyperparameter oder welche Parameter bestimmen die Performance eines DQN
wie wir schon gesehen habe gibt es unterschiedliche Parameter, welche wir oben beschrieben und welche einen direkten Einfluss auf das Lernverhalten des DQNs hat. Hier wollen wir einen Überblick über diese parameter schaffen.
Jeder dieser Hyperparameter kann die Leistung eines DQNs erheblich beeinflussen, und sie sind oft nicht unabhängig voneinander, was bedeutet, dass ihre Abstimmung eine komplexe Aufgabe sein kann. Techniken wie Grid Search, Random Search oder komplexere Optimierungsmethoden können für diesen Zweck verwendet werden.
Hier sind einige der Schlüssel-Hyperparameter bei DQNs.
Learning Rate (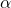 )
)
Die Learning Rate steuert, wie stark die Q-Wert-Schätzungen während des Trainings aktualisiert werden. Eine hohe Learning Rate bedeutet, dass das Netzwerk möglicherweise schnell lernt, aber auch das optimale Ergebnis überschießen könnte. Eine niedrige Learning Rate ermöglicht ein stabileres Lernen, allerdings auf die Gefahr hin, sehr langsam zu lernen.
Discount Factor (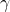 )
)
Der Discount Factor bestimmt die Bedeutung zukünftiger Belohnungen. Ein Discount Factor von 0 macht den Agenten „kurzsichtig“ (d.h. fokussiert nur auf unmittelbare Belohnungen), während ein Discount Factor nahe 1 darauf abzielt, langfristige Belohnungen zu erzielen. Der Wert von ( ![]() ) wird normalerweise zwischen 0,9 und 1 eingestellt.
) wird normalerweise zwischen 0,9 und 1 eingestellt.
Epsilon ( ) in (
) in ( )-Greedy Policy
)-Greedy Policy
Der Epsilon-Parameter in der (![]() )-Greedy Policy steuert den Kompromiss zwischen Exploration und Exploitation. Mit einer Wahrscheinlichkeit von (
)-Greedy Policy steuert den Kompromiss zwischen Exploration und Exploitation. Mit einer Wahrscheinlichkeit von ( ![]() ) wählt der Agent eine zufällige Aktion (Exploration) und mit einer Wahrscheinlichkeit von (
) wählt der Agent eine zufällige Aktion (Exploration) und mit einer Wahrscheinlichkeit von ( ![]() ) die Aktion mit dem höchsten geschätzten Q-Wert (Exploitation). (
) die Aktion mit dem höchsten geschätzten Q-Wert (Exploitation). ( ![]() ) könnte so eingestellt werden, dass es im Laufe der Zeit abnimmt, damit das Modell zuerst erkundet und dann das erlernte Wissen ausnutzt.
) könnte so eingestellt werden, dass es im Laufe der Zeit abnimmt, damit das Modell zuerst erkundet und dann das erlernte Wissen ausnutzt.
Batch Size
In DQNs werden Erfahrungen in einem Replay Buffer gespeichert und in Mini-Batches zum Trainieren des Netzwerks abgerufen. Die Batch Size bestimmt, wie viele Erfahrungen für jedes Update verwendet werden.
Replay Buffer Size
Der Replay Buffer speichert vergangene Erfahrungen, die zufällig ausgewählt werden, um das Netzwerk zu trainieren. Ein größerer Buffer kann eine vielfältigere Menge an Erfahrungen enthalten, benötigt jedoch mehr Speicher.
Target Network Update Frequency
DQNs verwenden ein separates Target Network, um das Training zu stabilisieren. Das Target Network ist eine Kopie des ursprünglichen Netzwerks, wird jedoch seltener aktualisiert. Dieser Hyperparameter steuert, wie oft das Target Network mit den Gewichten des Hauptnetzwerks aktualisiert wird.
Anzahl der Episoden und Schritte
Die Gesamtzahl der Episoden und die Schritte innerhalb jeder Episode können auch als Hyperparameter betrachtet werden. Sie definieren, wie lange der Agent trainiert wird.
Layer-Architektur und Aktivierungsfunktionen
Die Architektur des neuronalen Netzwerks selbst, einschließlich der Anzahl der Schichten, der Anzahl der Knoten in jeder Schicht und der Arten von Aktivierungsfunktionen, können alle als Hyperparameter betrachtet werden.
Reward Clipping
In einigen Implementierungen werden Belohnungen auf einen bestimmten Bereich beschränkt, um die Skalierung zu steuern und das Training stabiler zu machen.
Prioritized Experience Replay
Bei Verwendung von Prioritized Experience Replay kommen zusätzliche Hyperparameter wie der Importance Sampling Exponent ins Spiel.
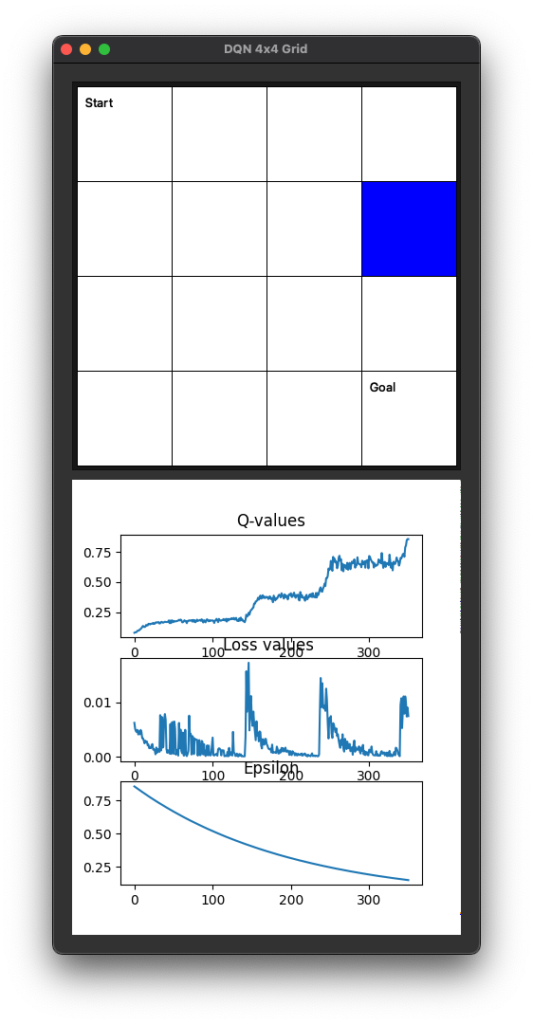
Python Beispiel
Nach dieser Einführung nun ein konkretes Beispiel in Python welches es ermöglich selbst mit der Konfiguration zu experimentieren.
import sys
import numpy as np
import random
import matplotlib.pyplot as plt
from matplotlib.backends.backend_qtagg import FigureCanvasQTAgg as FigureCanvas
from PyQt6.QtCore import Qt, QTimer
from PyQt6.QtWidgets import QApplication, QMainWindow, QGraphicsScene, QGraphicsView, QGraphicsRectItem, QVBoxLayout, QWidget
from PyQt6.QtGui import QBrush, QColor
import tensorflow as tf
# -------------- Hyperparameter Configuration ----------------
# ALPHA_START: Initial learning rate for the Adam optimizer
# ALPHA_MIN: Minimum learning rate to avoid overfitting as training progresses
# ALPHA_DECAY: Decay factor for learning rate, applied each episode
ALPHA_START = 0.001
ALPHA_MIN = 0.001
ALPHA_DECAY = 0.995
# GAMMA: Discount factor for future rewards in Q-Learning
GAMMA = 0.99
# EPSILON_START: Initial value for epsilon in epsilon-greedy exploration
# EPSILON_MIN: Minimum value for epsilon to maintain some level of exploration
# EPSILON_DECAY: Decay factor for epsilon, applied each episode
EPSILON_START = 1.0
EPSILON_MIN = 0.05
EPSILON_DECAY = 0.995
# MEMORY_SIZE: Max number of experiences stored in the replay memory
# BATCH_SIZE: Number of experiences sampled from memory to train the model
MEMORY_SIZE = 500
BATCH_SIZE = 32
# TRAINING_EPISODES: Number of episodes over which the model will be trained
TRAINING_EPISODES = 1000
# ----------------- Visualization Metrics ---------------------
# Initialize lists to store Q-values, Loss-values, and Epsilon-values for plotting
q_values_plot = []
loss_values_plot = []
epsilon_values_plot = []
# ----------------- Environment Configuration -----------------
# GRID_SIZE: Dimensions of the square grid environment
# STATE_SIZE: The total number of states in the grid (grid size squared)
# ACTION_SIZE: Number of possible actions (Up, Down, Left, Right)
GRID_SIZE = 4
STATE_SIZE = GRID_SIZE * GRID_SIZE
ACTION_SIZE = 4
GOAL_STATE = (GRID_SIZE-1, GRID_SIZE-1)
# ----------------- Replay Memory Initialization --------------
# Initialize an empty list to serve as the agent's experience replay memory
replay_memory = []
# ----------------- Deep Q-Network Architecture ----------------
# Build the DQN model using TensorFlow/Keras.
# Layer details:
# - Two hidden layers, each with 32 nodes and ReLU activation
# - Output layer with a node for each action, using linear activation
model = tf.keras.Sequential([
tf.keras.layers.Dense(32, activation='relu', input_shape=(STATE_SIZE,)),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dense(ACTION_SIZE, activation='linear')
])
# Initialize the Adam optimizer with the starting learning rate
optimizer = tf.keras.optimizers.legacy.Adam(learning_rate=ALPHA_START)
# Compile the model using Mean Squared Error as the loss function
model.compile(optimizer=optimizer, loss='mean_squared_error')
# ----------------- Target Network Initialization ---------------
# Initialize a target network with identical architecture and initial weights
# The target network is used for generating Q-value targets during training
target_model = tf.keras.models.clone_model(model)
target_model.set_weights(model.get_weights())
# Function to sync the target network with the main DQN model
def update_target_model():
target_model.set_weights(model.get_weights())
# --------------- Epsilon-Greedy Policy Definition ---------------
# Function to select an action using epsilon-greedy exploration strategy
# With probability epsilon, a random action is selected
# With probability 1-epsilon, the action with the highest Q-value is selected
def epsilon_greedy(state, epsilon):
if random.random() < epsilon:
return random.randint(0, ACTION_SIZE-1)
else:
q_values = model.predict(state.reshape(1, STATE_SIZE), verbose=0)
return np.argmax(q_values[0])
# Training function
def train_dqn():
# Access the global replay_memory variable to store experiences
global replay_memory
# Check if enough samples are available in replay_memory for training
if len(replay_memory) < BATCH_SIZE:
return # Not enough samples to train, exit the function
# Randomly sample a batch from the replay_memory
minibatch = random.sample(replay_memory, BATCH_SIZE)
# Unpack the elements of each experience in the minibatch
# Each tuple consists of (state, action, reward, next_state, done)
states, actions, rewards, next_states, dones = zip(*minibatch)
# Convert to NumPy arrays for efficient numerical operations
states = np.array(states)
next_states = np.array(next_states)
rewards = np.array(rewards)
dones = np.array(dones)
# Use the target model to predict the Q-values of the next_states
future_q_values = target_model.predict(next_states, verbose=0)
# Update the Q-values using the Bellman equation
# Q(s,a) = r + gamma * max[Q(s', a')] (if not done)
updated_q_values = rewards + GAMMA * np.max(future_q_values, axis=1) * (1 - dones)
# Get the current Q-values for the sampled states
current_q_values = model.predict(states, verbose=0)
# Update the Q-values with the newly computed values
for i, action in enumerate(actions):
current_q_values[i][action] = updated_q_values[i]
# Perform a gradient descent step on the loss between current and updated Q-values
history = model.train_on_batch(states, current_q_values)
# Return the mean Q-value and the training history for this batch
return np.mean(current_q_values), history
# GUI
app = QApplication([])
window = QWidget()
layout = QVBoxLayout()
window.setLayout(layout)
grid_view = QGraphicsView()
layout.addWidget(grid_view)
window.setWindowTitle("DQN 4x4 Grid")
grid_view.setFixedSize(410, 410)
scene = QGraphicsScene()
scene.setSceneRect(0, 0, 400, 400)
grid_view.setScene(scene)
fig, axs = plt.subplots(3, 1)
canvas = FigureCanvas(fig)
layout.addWidget(canvas)
window.show()
# Draw grid and agent
rectangles = {}
for i in range(GRID_SIZE):
for j in range(GRID_SIZE):
rect_item = scene.addRect(i*100, j*100, 100, 100)
rect_item.setPen(QColor(0, 0, 0))
rect_item.setBrush(QColor(255, 255, 255))
rectangles[(i, j)] = rect_item
agent_rect = scene.addRect(0, 0, 100, 100)
agent_rect.setBrush(QColor(0, 0, 255))
def update_agent_position(agent_state):
i, j = agent_state
agent_rect.setRect(i * 100, j * 100, 100, 100)
# Draw Start and Goal Labels
start_label = scene.addText("Start")
start_label.setPos(5, 5)
start_label.setDefaultTextColor(QColor(0, 0, 0))
goal_label = scene.addText("Goal")
goal_label.setPos((GRID_SIZE - 1) * 100 + 5, (GRID_SIZE - 1) * 100 + 5)
goal_label.setDefaultTextColor(QColor(0, 0, 0))
# Main Loop
epsilon = EPSILON_START # Initialize epsilon for epsilon-greedy policy
alpha = ALPHA_START # Initialize learning rate
goals_achieved = 0 # Counter for the number of times the agent achieves the goal
# Loop through each episode for training
for episode in range(1, TRAINING_EPISODES + 1):
state = np.zeros(STATE_SIZE) # Initialize state vector
agent_state = (0, 0) # Cartesian coordinates of the agent
state[0] = 1 # Mark initial position in the state vector
done = False # Flag to indicate if an episode is done
# Episode loop
while not done:
# GUI Update: Refresh the graphical interface
app.processEvents()
QTimer.singleShot(100, lambda: update_agent_position(agent_state))
# Decision Making: Choose an action using epsilon-greedy policy
action = epsilon_greedy(state, epsilon)
reward = 0 # Initialize reward
# Action Effect: Update the agent's state based on chosen action
x, y = agent_state
if action == 0: # Move Up
y = max(y - 1, 0)
elif action == 1: # Move Down
y = min(y + 1, GRID_SIZE - 1)
elif action == 2: # Move Left
x = max(x - 1, 0)
elif action == 3: # Move Right
x = min(x + 1, GRID_SIZE - 1)
# Check Goal State: Determine if the agent reached the goal
new_agent_state = (x, y)
if new_agent_state == GOAL_STATE:
reward = 1
done = True # Episode ends
# State Representation: Convert Cartesian coordinates to state vector
next_state = np.zeros(STATE_SIZE)
next_state[x + y * GRID_SIZE] = 1
# Experience Storage: Store transition in replay memory
replay_memory.append((state, action, reward, next_state, done))
replay_memory = replay_memory[-MEMORY_SIZE:] # Trim to fit memory size
# Model Training: Train the DQN based on stored experiences
result = train_dqn()
if result:
mean_q_value, loss_value = result
q_values_plot.append(mean_q_value)
loss_values_plot.append(loss_value)
epsilon_values_plot.append(epsilon)
# State Update: Move to the next state
state = next_state
agent_state = new_agent_state
# Epsilon Update: Decay epsilon for exploration-exploitation tradeoff
epsilon = max(EPSILON_MIN, epsilon * EPSILON_DECAY)
# Target Model Update: Sync target model with main model periodically
if episode % 5 == 0:
update_target_model()
# Learning Rate Update: Decay learning rate over time
alpha = max(ALPHA_MIN, alpha * ALPHA_DECAY)
tf.keras.backend.set_value(model.optimizer.learning_rate, alpha)
# Goal Count: Increment if the agent reached the goal during this episode
if agent_state == GOAL_STATE:
goals_achieved += 1
print(f"Episode: {episode}, Epsilon: {epsilon}, Goals achieved: {goals_achieved}")
axs[0].clear()
axs[0].plot(q_values_plot)
axs[0].set_title("Q-values")
axs[1].clear()
axs[1].plot(loss_values_plot)
axs[1].set_title("Loss values ")
axs[2].clear()
axs[2].plot(epsilon_values_plot)
axs[2].set_title("Epsilon")
canvas.draw()
sys.exit(app.exec())