Inhalt
Deep Q-Networks für den Aktienhandel: Ein Python-Beispiel mit Yahoo Finance und TensorFlow
Disclaimer: Dieser Python-Code bietet einen einfachen Ansatz für den Einstieg in algorithmischen Handel mit DQN. Es ist jedoch wichtig zu betonen, dass dieser Code zu Anschauchungszwecken und nicht für den realen Handel ausgelegt ist. Investitionen in den Aktienmarkt sind riskant und sollten nur mit entsprechender Vorsicht und Expertise getätigt werden.
Die Artikel entstand als erstes Konzept für Grundüberlegungen.
Im vorhergehenden Beitrag „Deep-Q-Networks: Eine Revolution im Reinforcement Learning“ haben wir uns mit den Grundlagen von Deep-Q-Netzwerken beschäftigt. Nun wollen wir dieses Wissen versuchsweise auf die Problemstellung des Aktienhandels anwenden.
Das Ziel ist es hierbei, mithilfe eines DQN-Modells Handelsstrategien zu entwickeln, die den Gesamtertrag optimieren können.
Zu Beginn soll es sich um eine einzelne Aktie (AAPL) handeln, bei welcher wir versuchen die Aktionen (Kaufen, Halten, Verkaufen) so auszuführen, dass wir einen möglichst großen Gewinn in einem simulierten Portfolio erhalten. Dinge wie Transaktionskosten oder Mindestbetrag beim Kauf lassen wir zu Gunsten des Verständnisses erstmal außer acht.
Grundlegende Methodische Vorgehensweise:
- Datensammlung: Zuallererst werden historische Aktienkurse und andere relevante Daten gesammelt. Diese Daten dienen als Trainingsgrundlage für das DQN-Modell.
- Vorverarbeitung: Die gesammelten Daten werden normalisiert und für das Training aufbereitet.
- DQN-Architektur: unser bekannter Aufbau mit zwei neuronalen Netzwerken.
- Training: Der Agent interagiert mit der Umgebung, indem er Aktionen basierend auf der aktuellen Politik ausführt. Die erzielten Belohnungen und der neue Zustand der Umgebung werden dann verwendet, um das Modell zu aktualisieren. Dies wird über mehrere Epochen hinweg wiederholt.
- Policy-Optimierung: Während des Trainings wird die Strategie (Policy) des Agents laufend angepasst, um die erwarteten zukünftigen Belohnungen zu maximieren.
- Backtesting: Die Leistung des DQN-Modells wird anhand historischer Daten überprüft. Dies ist entscheidend, um die Tauglichkeit des Modells für den Live-Einsatz zu bewerten.
Schlüsselkomponenten
Datenabruf mit Yahoo Finance
Zuerst holen wir die historischen Schlusskurse der AAPL-Aktie für einen Zeitraum mit dem yfinance-Paket. Dieser Datensatz dient als Grundlage für das Training des Modells und kann später auch für das Backtesting mit anderen Daten verwendet werden.
def fetch_stock_data(ticker, start_date, end_date):
stock_data = yf.download(ticker, start=start_date, end=end_date)
return stock_data['Close'].valuesDatenaufbereitung
Die gesammelten Daten werden normalisiert, um das Netzwerktraining zu erleichtern.
def normalize_data(data):
return (data - np.min(data)) / (np.max(data) - np.min(data))Die Normalisierung ist ein wichtiger Schritt in der Datenvorbereitung, insbesondere wenn neuronale Netze oder andere Machine-Learning-Modelle im Spiel sind. Ziel der Normalisierung ist es, die Daten so zu skalieren, dass sie in einem bestimmten Bereich liegen, meist zwischen 0 und 1 oder -1 und 1. Dies macht es dem Algorithmus leichter, Muster in den Daten zu erkennen und das Modell effizienter zu trainieren.
Warum ist Normalisierung wichtig?
Unskalierte oder unterschiedlich skalierte Features (in unserem Fall ist dies ein singuläres nämlich der Schlusswert) können dazu führen, dass das Modell nicht optimal trainiert wird. Beispielsweise könnten die Aktienkurse in einer großen Zahlenreihe wie Hunderten oder Tausenden liegen, während andere Features wie Handelsvolumen oder Durchschnitte in anderen Größenordnungen liegen könnten. Durch die Normalisierung wird sichergestellt, dass keine Variablen aufgrund ihrer Größenordnung übermäßig das Training beeinflussen.
Min-Max-Normalisierung
Im vorliegenden Code wird die Min-Max-Normalisierung verwendet, die eine der einfachsten und am häufigsten verwendeten Techniken ist. Die Formel für die Min-Max-Normalisierung ist:
![]()
In Python könnte dies wie folgt implementiert werden:
def normalize_data(data):
return (data - np.min(data)) / (np.max(data) - np.min(data))Beispiel
Angenommen, wir haben AAPL-Aktienpreise für eine bestimmte Woche wie folgt: [150, 152, 154, 153, 151].
- Der minimale Preis ist 150 und der maximale Preis ist 154.
- Wir wenden die Min-Max-Normalisierung auf jeden Wert an:
- (
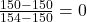 )
) - (
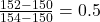 )
) - (
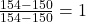 )
) - (
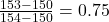 )
) - (
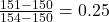 )
)
- (
Jetzt hat man die normalisierten Werte [0, 0.5, 1, 0.75, 0.25], die alle im Bereich zwischen 0 und 1 liegen. Diese skalierten Werte werden dann als Input für das neuronale Netz verwendet.
Zusammengefasst ist die Normalisierung ist ein wichtiger Schritt, um sicherzustellen, dass das Modell effizient und effektiv trainiert wird. Durch die Skalierung aller Werte in einen definierten Bereich können wir sicherstellen, dass alle Features gleichmäßig zum Training des Modells beitragen.
Erstellung des DQN-Modells
Das DQN-Modell wird mit TensorFlow implementiert und besteht aus einer Sequenz von vollständig vernetzten Schichten.
def build_dqn_model(input_shape, n_actions):
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape=input_shape),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dense(n_actions, activation='linear')
])
model.compile(optimizer='adam', loss='mse')
return modelTraining des Modells
Das Modell wird über mehrere Episoden trainiert. In jedem Schritt wird eine Aktion (Kaufen, Verkaufen, Halten) gewählt und der zugehörige Ertrag berechnet. Die Erfahrungen werden in einem Replay-Speicher gespeichert, aus dem zufällige Stichproben für das Training gezogen werden.
Beim 4×4 Grid-Labyrinth konnte das Netzwerk auf ein konkretes und absolutes Ziel hin trainiert werden – das Erreichen des Ziel-Feldes. Danach konnte das Lernen ausgelegt werden. In Falle von Aktienwerten haben wir kein absolutes Ziel sondern versuchen uns der best möglichen Strategie anzunähern. Somit durchlaufen wir ständig den Zeitraum neu und „probieren“ uns durch die unterschiedlichen Möglichkeiten. Am Ende einer jeden Episode aktualisieren wir das Target-Network. Je mehr Episoden wir also ausführen desto besser (aller Voraussicht nach) wird unsere DQN-Anlagestrategie werden.
# Main function to train DQN
def main():
# Constants
EPISODES = 20
WINDOW_SIZE = 10
BATCH_SIZE = 32
N_ACTIONS = 3 # 0: Hold, 1: Buy, 2: Sell
# Fetch and normalize stock data
train_start_date = "2020-01-01"
train_end_date = "2021-01-01"
stock_data = fetch_stock_data("AAPL", train_start_date, train_end_date)
stock_data = normalize_data(stock_data)
# Build DQN model
model = build_dqn_model((WINDOW_SIZE,), N_ACTIONS)
target_model = build_dqn_model((WINDOW_SIZE,), N_ACTIONS)
target_model.set_weights(model.get_weights())
# Initialize replay memory
replay_memory = []
for episode in range(EPISODES):
print(f"Episode {episode + 1}/{EPISODES}")
# Initial state
state = stock_data[:WINDOW_SIZE]
total_profit = 0
done = False
for t in range(WINDOW_SIZE, len(stock_data) - 1):
# Select action using epsilon-greedy policy
if random.random() < 0.1:
action = random.randint(0, N_ACTIONS - 1)
else:
action = np.argmax(model.predict(state.reshape((1, WINDOW_SIZE)), verbose=0))
# Execute action and observe new state and reward
next_state = stock_data[t - WINDOW_SIZE + 1:t + 1]
reward = 0
if action == 1: # Buy
reward = stock_data[t + 1] - stock_data[t]
elif action == 2: # Sell
reward = stock_data[t] - stock_data[t + 1]
total_profit += reward
done = True if t == len(stock_data) - 2 else False
# Store transition in replay memory
replay_memory.append((state, action, reward, next_state, done))
state = next_state
# Sample random batch from replay memory
if len(replay_memory) > BATCH_SIZE:
batch = random.sample(replay_memory, BATCH_SIZE)
states, actions, rewards, next_states, dones = zip(*batch)
# Compute target Q-values
targets = model.predict(np.array(states), verbose=0)
next_targets = target_model.predict(np.array(next_states), verbose=0)
for i in range(BATCH_SIZE):
targets[i][actions[i]] = rewards[i] + (1 - dones[i]) * 0.99 * np.max(next_targets[i])
# Update Q-values
model.fit(np.array(states), targets, epochs=1, verbose=0)
# Update target model
target_model.set_weights(model.get_weights())
print(f"Episode {episode + 1}/{EPISODES} - Total Profit: {total_profit}")Der Hauptteil des Trainingsprozesses in einem DQN (Deep Q-Network) findet während der Episoden statt. Jede Episode stellt eine Durchlauf des Trainingsdatensatzes dar. In unserem Fall ist eine Episode eine vollständige Durchführung des Algorithmus durch die AAPL Aktienkurse für ein Jahr. Im Folgenden erkläre ich, was in deinem Code während einer einzelnen Episode geschieht:
- Initialisierung der Anfangszustände und Variablen:
Der Anfangszustand (state) wird als die ersten WINDOW_SIZE (in deinem Code 10) Datenpunkte des normalisierten Aktienpreises festgelegt.
Die Variable total_profit wird auf null gesetzt.
- Aktionsauswahl und -durchführung:
Für jede Zeit t im Datensatz (beginnend nach dem WINDOW_SIZE-ten Datenpunkt) wird eine Aktion gewählt.
Die Aktion wird nach der Epsilon-Greedy-Strategie gewählt: Mit einer Wahrscheinlichkeit von 0.1 wird eine zufällige Aktion gewählt; ansonsten wird die Aktion gewählt, die den höchsten Q-Wert hat, basierend auf dem aktuellen Zustand.
- Berechnung der Belohnung und des neuen Zustands:
Nach der Ausführung der Aktion wird die Belohnung (reward) berechnet.
Der neue Zustand (next_state) wird ebenfalls berechnet, indem der nächste Datenpunkt in das Fenster aufgenommen und der älteste entfernt wird.
- Replay Memory und Batch-Training:
Die Erfahrung (bestehend aus state, action, reward, next_state, done) wird im Replay Memory gespeichert.
Wenn das Replay Memory groß genug ist, wird eine zufällige Stichprobe (batch) daraus für das Training genommen.
Das Modell wird dann anhand dieses Batches trainiert, um die Q-Werte zu aktualisieren.
- Aktualisierung des Ziellmodells:
Nach dem Durchlauf durch den gesamten Datensatz werden die Gewichtungen des Zielmodells (target_model) mit den Gewichtungen des Hauptmodells (model) aktualisiert.
- Zusammenfassung der Episode:
Am Ende der Episode wird der total_profit für diese Episode ausgegeben.
Durch den Durchlauf mehrerer Episoden lernt das Netzwerk schrittweise, welche Aktionen in welchen Zuständen vorteilhaft sind, um den kumulativen Gewinn zu maximieren und wir aktualisieren unser Target-Netzwerk.
Der Trainingscode: komplett
Nach dem erfolgreichen Training wird das Model automatisch als „den_aapl_model.h5“ gespeichert. Wer eine Version zum weiteren Testen sucht, kann eine Version hier herunterladen.
import yfinance as yf
import numpy as np
import tensorflow as tf
import random
# Fetch historical data for AAPL stock
def fetch_stock_data(ticker, start_date, end_date):
stock_data = yf.download(ticker, start=start_date, end=end_date)
return stock_data['Close'].values
# Normalize the stock data
def normalize_data(data):
return (data - np.min(data)) / (np.max(data) - np.min(data))
# Create DQN model
def build_dqn_model(input_shape, n_actions):
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape=input_shape),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dense(n_actions, activation='linear')
])
model.compile(optimizer='adam', loss='mse')
return model
# Main function to train DQN
def main():
# Constants
EPISODES = 20
WINDOW_SIZE = 10
BATCH_SIZE = 32
N_ACTIONS = 3 # 0: Hold, 1: Buy, 2: Sell
# Fetch and normalize stock data
train_start_date = "2020-01-01"
train_end_date = "2021-01-01"
stock_data = fetch_stock_data("AAPL", train_start_date, train_end_date)
stock_data = normalize_data(stock_data)
# Build DQN model
model = build_dqn_model((WINDOW_SIZE,), N_ACTIONS)
target_model = build_dqn_model((WINDOW_SIZE,), N_ACTIONS)
target_model.set_weights(model.get_weights())
# Initialize replay memory
replay_memory = []
for episode in range(EPISODES):
print(f"Episode {episode + 1}/{EPISODES}")
# Initial state
state = stock_data[:WINDOW_SIZE]
total_profit = 0
done = False
for t in range(WINDOW_SIZE, len(stock_data) - 1):
# Select action using epsilon-greedy policy
if random.random() < 0.1:
action = random.randint(0, N_ACTIONS - 1)
else:
action = np.argmax(model.predict(state.reshape((1, WINDOW_SIZE)), verbose=0))
# Execute action and observe new state and reward
next_state = stock_data[t - WINDOW_SIZE + 1:t + 1]
reward = 0
if action == 1: # Buy
reward = stock_data[t + 1] - stock_data[t]
elif action == 2: # Sell
reward = stock_data[t] - stock_data[t + 1]
total_profit += reward
done = True if t == len(stock_data) - 2 else False
# Store transition in replay memory
replay_memory.append((state, action, reward, next_state, done))
state = next_state
# Sample random batch from replay memory
if len(replay_memory) > BATCH_SIZE:
batch = random.sample(replay_memory, BATCH_SIZE)
states, actions, rewards, next_states, dones = zip(*batch)
# Compute target Q-values
targets = model.predict(np.array(states), verbose=0)
next_targets = target_model.predict(np.array(next_states), verbose=0)
for i in range(BATCH_SIZE):
targets[i][actions[i]] = rewards[i] + (1 - dones[i]) * 0.99 * np.max(next_targets[i])
# Update Q-values
model.fit(np.array(states), targets, epochs=1, verbose=0)
# Update target model
target_model.set_weights(model.get_weights())
print(f"Episode {episode + 1}/{EPISODES} - Total Profit: {total_profit}")
# Save the model
model.save('dqn_aapl_model.h5')
if __name__ == "__main__":
main()
Backtesting: Simulation
Nachdem wir nun ein Modell auf den Daten von 2020 trainiert haben, wollen wir natürlich auch schauen wie performant das Modell ist mit neuen Daten ist.
import yfinance as yf
import numpy as np
import tensorflow as tf
def fetch_stock_data(ticker, start_date, end_date):
stock_data = yf.download(ticker, start=start_date, end=end_date)
return stock_data['Close'].values
def normalize_data(data):
return (data - np.min(data)) / (np.max(data) - np.min(data))
def test_model(model, stock_data, window_size=10, initial_capital=10):
state = stock_data[:window_size] # Initial state
cash = initial_capital # Starting capital
stock_quantity = 0 # Number of shares of stock owned
print("Starting Portfolio Value: ", initial_capital)
for t in range(window_size, len(stock_data) - 1):
# Predict the best action using the trained DQN model
action = np.argmax(model.predict(state.reshape((1, window_size)), verbose=0))
# Calculate current portfolio value
portfolio_value = cash + stock_data[t] * stock_quantity
portfolio_value_change = (portfolio_value * 100 / initial_capital)-100
print(f"Currency is normalized!")
print(f"Time Step {t}")
print(f"Current Portfolio Value: {portfolio_value:.2f} - Change: {portfolio_value_change:.2f}%")
print(f"Stock Price: {stock_data[t]:.2f}")
if action == 0: # Hold
print("Action: Hold")
elif action == 1: # Buy
if cash > stock_data[t]:
stock_quantity += 1
cash -= stock_data[t]
print(f"Action: Buy, New Stock Quantity: {stock_quantity}, Remaining Cash: {cash:.2f}")
else:
print("Action: Want to Buy, but not enough cash.")
elif action == 2: # Sell
if stock_quantity > 0:
stock_quantity -= 1
cash += stock_data[t]
print(f"Action: Sell, New Stock Quantity: {stock_quantity}, Remaining Cash: {cash:.2f}")
else:
print("Action: Want to Sell, but don't own any stock.")
# Shift the state window to include data for the next time step
state = stock_data[t - window_size + 1:t + 1]
print("-----------------------------------------------------------")
# Load the trained model
model_path = "dqn_aapl_model.h5" # Replace with the path to your saved model
loaded_model = tf.keras.models.load_model(model_path)
# Fetch and normalize historical stock data
test_start_date = "2021-01-02"
test_end_date = "2022-01-01"
stock_data = fetch_stock_data("AAPL", test_start_date, test_end_date)
stock_data = normalize_data(stock_data)
# Test the trained model
test_model(loaded_model, stock_data)
Und wie sieht das Ergebnis aus?
-----------------------------------------------------------
Currency is normalized!
Time Step 250
Current Portfolio Value: 19.77 - Change: 97.74%
Stock Price: 0.97
Action: Sell, New Stock Quantity: 18, Remaining Cash: 2.37
-----------------------------------------------------------Dies ist natürlich nur eine Simulation und lässt u.a. einige Parameter bzgl. der Kosten etc. außer acht. Damit ist das Ergebnis zwar beeindruckend, bildet aber die Realität nicht ab. Wäre es so einfach, würde vermutlich jeder der ein wenig programmieren kann nichts anderes mehr machen.
In weiteren Beiträgen wollen wir an diesem Modell arbeiten und die Grundzüge erweitern.
Mögliche Verbesserungen
- Einschließen aller Kostenfaktoren bzw. Kaufbedingungen
- Risikomanagement
- Komplexere Belohnungsfunktion
- Implementierung weiterer Features (Aktienkennzahlen)
- Aufbau der neuronalen Netzwerke
- Tuning der Hyperparameter (ggf. ebenfalls durch ein neuronales Netz gesteuert)