Big Bang || Big Bounce

The conservation law for the angular momentum in curved spacetime requires that the antisymmetric part of the affine connection (the torsion tensor) is a variable in the principle of least action. The coupling between spin and torsion generates gravitational repulsion in fermionic matter at extremely high densities and avoids the formation of singularities in black holes. We show that every black hole in the presence of torsion forms a nonsingular, closed, nearly flat, homogeneous, and isotropic universe on the other side of its event horizon. Quantum particle production in such a universe can generate a period of exponential expansion which creates an enormous amount of matter in that universe. Accordingly, our Universe may have originated from the interior of a black hole existing in another universe.
“Nikodem Popławski” – https://doi.org/10.48550/arXiv.1410.3881

Der theoretische Physiker Nikodem Poplawski kratz an einem Bild, welches im Allgemeinwissen gesetzt scheint wie die antike Annahme, dass das Atom das elementarste Objekt des Kosmos darstellt.

Der Versuch, selbst in der Vorstellung, in der Zeit zurück zu gehen zu dem Zeitpunkt, den wir als Ursprung bezeichnen, verursacht Kopfschmerzen, denn hier verändern sich die physikalischen Gesetzte grundlegend.

Vermutlich weit verbreitet ist die Vorstellung, dass da etwas am Anfang war, eine punktförmige Singularität, ein “Etwas”, das explodierte im “Big Bang” und über unvorstellbare Zeit unser heutiges Universum formte. Wirklich begreifen lässt sich dies mit unserem heutigen Wissen und Verstand nicht, sodass dieser Vorstellung auch etwas von Glauben anhaftet, denn auch mathematisch beschreiben lässt sich dieser Punkt bis heute nicht, aber er wird fieberhaft erkundet.

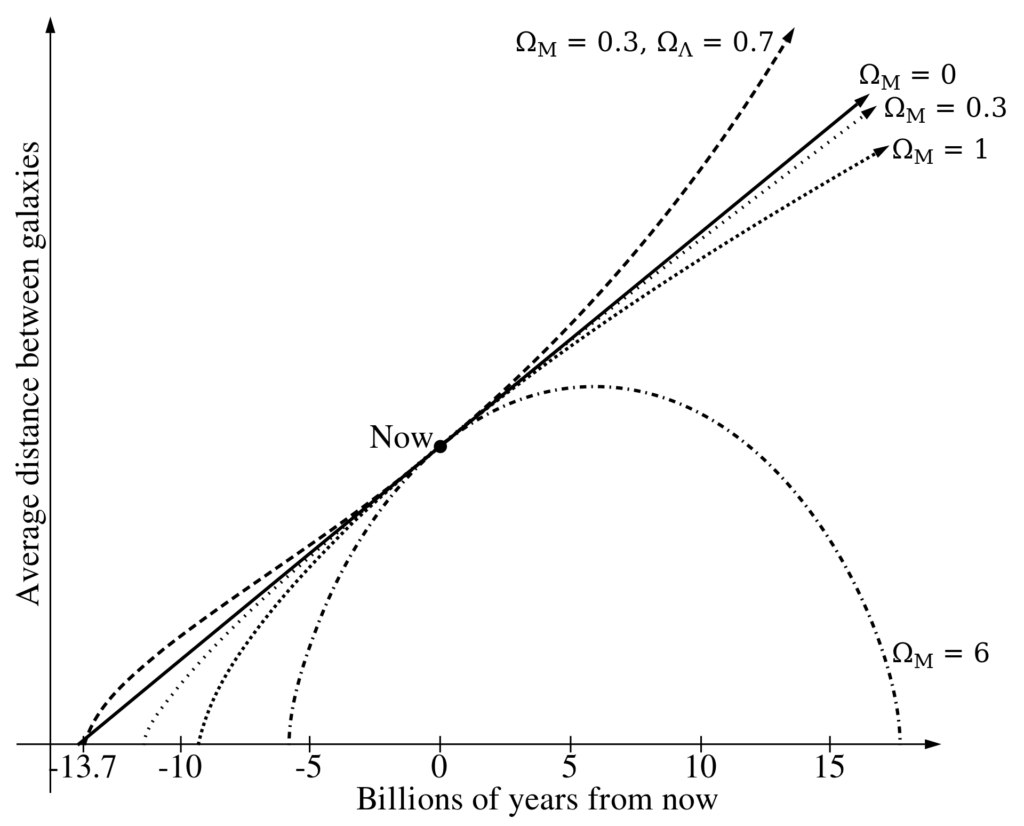
Gedankenexperiment: Bedenkt man das Gesetz der Entropie, nach welchem das Universum zu streben scheint, stellt sich die Frage nach dem endgültigen Schicksal des Universums (“Ultimate fate of the universe”). Wenn die Entropie jegliche höhere Ordnung zerlegt hat, könnte es je nach Zusammensetzung dazu führen, dass es implodiert (“Big Crunch”) und vielleicht auch wieder anschließend in einem neuen “Big Bang” als neues Universum expandiert und sich so ein Zyklus bildet.

Das endgültige Schicksal des Universums hängt von der
Massedichte $\Omega _{M}$ als auch der Dichte der dunklen Energie $\Omega _{\Lambda }$
(**Friedmann-Lemaître-Gleichung** nach BenRG)

{\displaystyle \Omega _{M}} — Das endgültige Schicksal des Universums hängt von der
Massedichte $\Omega _{M}$ als auch der Dichte der dunklen Energie $\Omega _{\Lambda }$
(**Friedmann-Lemaître-Gleichung** nach BenRG)

Über dieser Vorstellung hinaus gibt es vieles weitere Interessante Ideen und Ansätze über die Vergangenheit und den Weg des Universums. Wer sucht der findet.

Nun soll es aber um die expliziten Gedanken des Herrn Popławski gehen.

Der theoretische Ansatz ist hier die allgemeine Relativitätstheorie (AR), welche in der Kosmologie unter anderem die Gravitation und Krümmung der Raumzeit beschreibt. Für das gemeine, heutige Universum ist die AR ausreichend und kann auch die meisten Gesetzmäßigkeiten der Kosmologie und deren Phänomene beschreiben. Problematisch wird es jedoch an den Grenzzonen der Universums, sei es dessen Anfang aber auch an Punkten mit unglaublich hoher Massendichte wie es bei schwarzen Löchern der Fall ist. Plötzlich herrschen andere Bedingungen, welche einen großen Einfluss auf die Physik zu haben scheinen und der AR ihrer Beschreibungskraft berauben.

Hier wird es notwendig die Quantenmechanik (QM) zu bemühen. Diese hat jedoch mit einer Vorhersage der AR ein Problem: Singularitäten. Dies wären Punkte im Universum, unendlich klein und unendlich dicht. Eine mögliche Lösung des Problems wäre die Quantengravitation.

Hier kommt nun die Einstein-Cartan-Sciama-Kibble-Theorie (ECSK) welche eine Verallgemeinerung der bereits allgemeinen Relativitätstheorie darstellt hinzu. Das Besondere dieser Theorie ist, das ein zusätzlicher Freiheitsgrad in Form der Torsion auftaucht, was in der ECSK zu einer zusätzlichen Feldgleichung führt. Die Torsion wird wiederum an den Spindichtetensor gekoppelt.

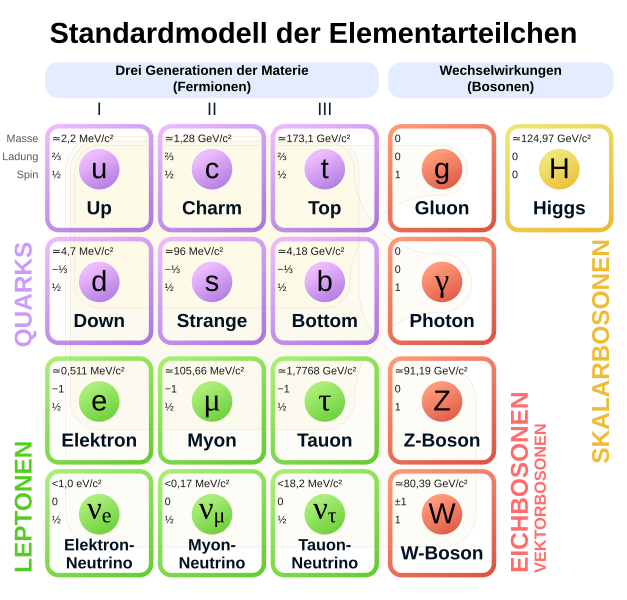
Nun steht ein Framework zur Verfügung mit welchem experimentiert und das auf speziellere Fälle angewandt kann. Die Interpretationsüberlegung von Poplawski bedient sich als Ausgangspunkt der Fermionengruppe (also im Grunde alle Teilchen welche im Standardmodell die Materieteilchen bilden). In dieser Gruppe geht es nun insbesondere um eine Eigenschaft des Spins (Eigendrehimpuls) der Teilchen.

Mathematisch drückt sich bezüglich der Gravitation die Verbindung des Spins und der Torsion in der ECSK Theorie folgendermaßen aus:

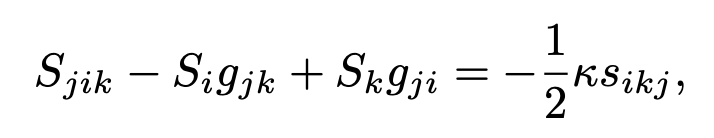
Ableiten lässt sich hieraus, dass die Torsion (Tensor $s_{ikj}$ ) proprotional zur Spindichte ist. Bei weiterer Analyse der Gleichung und Spezialfallanwendung stellt sich heraus, dass sich die ECSK ab einer Massendichte von $>10^{45} kg/m^3$ deutlich von der AR unterscheidet. Im Vakuum hingegen verändern sich die Gleichung der ECSK dahingehend, dass die denen der AR gleichen.

Diese Koppelung ist es nun, welche eine Singularität verbietet und neue Universen ermöglicht. Dies bedeutet, in einem System, in welchem eine sehr hohe Spindichte herrscht spielt die Torsion eine so große Rolle, das sie schließlich in der Energiedichtebetrachtung zu einer abstoßenden Kraft führt, welche der Gravitation entgegengewirkt (repulsive Gravitation). Somit gibt es eine natürliche Grenze, nämlich die Dichte $>10^{45} kg/m^3$ (O1) welche nicht überschritten werden kann, da es hier zu einer Gravitationsumkehr kommt.

Erklären lässt sich dies, wenn man Dirac Partikel als Quantenspinflüssigkeit betrachtet. In diesem Spezialfall ist die quadratische Spindichte einer Fermionenflüssigkeit:

quadratische Spindichte einer Fermionenflüssigkeit

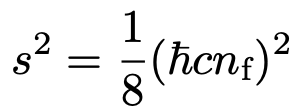
Die Fermionendichte $n_{f}$ geht hierbei quadratisch in die Gleichung ein, was erklärt, warum dies erst bei entsprechender Dichte eine relevante Rolle spielt.

Die Energiedichte als auch der Druck lassen sich hier darstellen als:

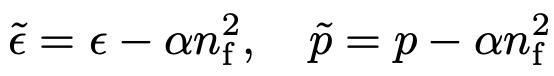
mit

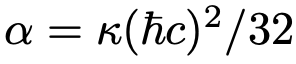
Unter der Annahme eines geschlossenen, homogenen und iostropischen Universums lassen sich die folgenden Friedman-Gleichungen (diese Beschreiben die zeitliche Entwicklung des Universums Vgl. 1. Abbildung) aufstellen:

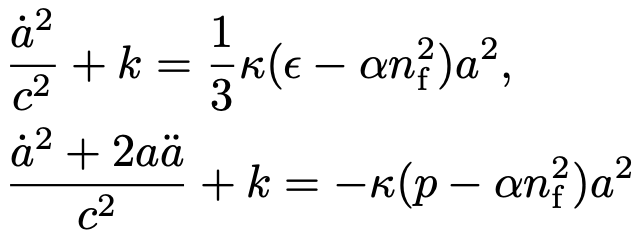
Nun wird ersichtlich, dass der Spin als auch die Torsion zur Energiedichte $\varepsilon$ als auch Druck $p$ mit einem negativen Term, welcher proportional zum Quadrat der Fermionenanzahl ist, beitragen und so wie eine abstoßende Gravitation wirken.

Ausflug in ein schwarzes Loch

Fliegen wir also in unserer Vorstellung los und machen und auf in ein schwarzes Loch (nehmen wir hierzu die Region Sagittarius A* welche wohl das Nächstliegende zu uns beherbergt). Nähern wir uns ihm und lassen wir uns hinter den Ereignishorizont (EH) ziehen. In der Theorie von Poplawski verschwinden wir nun nicht wie bisher angenommen in einer Singularität. Die Torsion sorgt dafür, dass wir durch die abstoßende Gravitationskomponente, welche bei diesen hohen Dichten entsteht, wie durch einen sehr dünnen Strudel gezogen werden und am anderen Ende wieder ausgespuckt werden. Er zeigt das gerne an einem anschaulichen Beispiel mit zwei Flaschen, welche mit einem kleinen Schlauch miteinander verbunden werden. In die eine Flasche wird Wasser gefüllt und das Wasser zur Rotation gebracht. Anschließend wird das Gebilde umgedreht.

Zunächst reicht vielleicht die Kraft der Rotation noch aus um das Wasser in der oberen Flasche zu halten, je näher jedoch das Wasser dem Übergang der zwei Flaschen kommt desto mehr ändert sich das Kraftverhältnis und was man beim Durchritt des Wassers in die andere Flasche sehen kann ist nicht, dass es einfach nur senkrecht hindurch fällt, sondern, dass es sich dort wieder wie ein Schirm ausbreitet (also wie die “Inflation” des oberen Modells). Und ja dies würde einer Ernsten-Rosen Brücke, respektive einem Wurmloch auf eine andere Seite entsprechen (Der Star-Trek-Moment).

Jetzt darf man seiner Fantasie freien Lauf lassen und sich überlegen, was sich dahinter verbirgt, ein anderes Universum? Und würde das bedeuten, dass hinter jedem schwarzen Loch eine neue Welt wartet? Nichts kann einem schwarzen Loch entkommen, nicht einmal Licht. Somit ist es und auch nicht möglich, mit den uns bisher bekannten Techniken hinter den Ereignishorizont zu sehen. Hier sind wir blind. Und selbst wenn jemand verrückt genug wäre, sich in eines hinein zu katapultieren, so würde es nie einen Bericht geben, der uns erreicht.

Durch diese Theorie entstehen weitere interessante Implikationen:

Durch die Einstein-Rosen-Brücke und die Idee, dass jegliche Materie die durch ein schwarzes Loch hindurch geht in einem neuen Universum landet, wäre das Schwarze-Loch-Informations-Paradoxon zu erklären
Da hiermit auch erklärbar wäre, warum der Ereignishorizont eine Einbahnstraße ist würde sich vielleicht auch erklären, warum Zeit asymmetrisch ist und nur in eine Richtung fließen kann