UMAP, kurz für „Uniform Manifold Approximation and Projection“, ist eine starke Methode zur Dimensionsreduktion und hat sich in der Datenwissenschaft rasch einen Namen gemacht. Im Gegensatz zu anderen gängigen Techniken, wie zum Beispiel t-SNE, basiert UMAP auf soliden mathematischen Grundlagen und bietet sowohl Geschwindigkeit als auch Flexibilität. Es wurde entwickelt, um hochdimensionale Daten in einen niedrigeren Dimensionenraum zu projizieren, wobei die ursprünglichen Abstände zwischen den Datenpunkten so gut wie möglich beibehalten werden. Dies ist besonders nützlich in Bereichen wie der Genomik, der Bildverarbeitung oder jeder anderen Disziplin, die mit hochdimensionalen Datensätzen arbeitet. Ein weiterer Vorteil von UMAP ist seine Anpassungsfähigkeit. Es kann nicht nur zur Dimensionsreduktion verwendet werden, sondern auch zum Clustering oder sogar zum semiüberwachten Lernen. Trotz seiner Komplexität ist UMAP erstaunlich intuitiv und kann ohne tiefe Kenntnisse der zugrunde liegenden Mathematik verwendet werden. Es ist ein Werkzeug, das sowohl für Datenwissenschaftler als auch für Neulinge in der Branche von unschätzbarem Wert ist.

Inhalt

Grundlagen Idee der Mathematik hinter der UMAP

die Dimensionsreduktion und basiert auf einer soliden mathematischen Grundlage, die von der topologischen Datenanalyse inspiriert ist. Die Grundidee von UMAP besteht darin, die Daten so in einen Raum niedriger Dimensionalität zu projizieren, dass die geometrische Struktur der Daten so gut wie möglich erhalten bleibt. Eine vereinfachte Erklärung der mathematischen Logik hinter UMAP:

1. Topologische Räume und Mannigfaltigkeiten

Die Datenpunkte in einem hochdimensionalen Raum können oft als eine Art „glattes“ Gebilde betrachtet werden, das als Mannigfaltigkeit bezeichnet wird. Eine Mannigfaltigkeit ist ein topologischer Raum, der lokal wie ein Euklidischer Raum aussieht. UMAP versucht, diese Mannigfaltigkeit zu identifizieren und ihre Struktur im niedrigerdimensionalen Raum zu bewahren.

Ein Manifold kann als eine „verzerrte“ Oberfläche in einem hochdimensionalen Raum betrachtet werden. Wenn man sich auf kleine Teile des Manifolds konzentriert, scheinen diese Teile flach zu sein, ähnlich wie ein kleines Stück Papier auf einer Kugel.

Beispiel: Stellen Sie sich vor, Sie haben eine Karte der Erde. Die Erdoberfläche ist ein 2D-Manifold in einem 3D-Raum. Lokal gesehen (z.B. auf der Karte einer Stadt) scheint die Erde flach zu sein, obwohl sie in Wirklichkeit eine Kugel ist.

2. Fuzzy Simplices Sets

UMAP nutzt die Theorie der „fuzzy simplicial sets“ (FSS), um die Datenstruktur zu modellieren. Ein „simplicial set“ ist eine Sammlung von Punkten, Linien, Dreiecken und so weiter, die zusammen eine topologische Struktur bilden.

Durch die Verwendung von FSS kann UMAP die Unsicherheit und den Rauschanteil in Daten berücksichtigen, was zu robusteren Ergebnissen führt.

Ein simplicial set besteht aus Punkten (0-Simplizes), Linien zwischen Punkten (1-Simplizes), Dreiecken (2-Simplizes) und so weiter. „Fuzzy“ bedeutet, dass es eine Unsicherheit darüber gibt, welche Punkte miteinander verbunden sind.

Beispiel: Stellen Sie sich eine Gruppe von Punkten vor, die Sterne am Himmel repräsentieren. Einige Sterne sind durch Linien verbunden, um Sternbilder zu bilden (dies sind die 1-Simplizes). In UMAP gibt es eine Unsicherheit darüber, welche Sterne tatsächlich verbunden sind, daher das „fuzzy“.

3. K-Nächste-Nachbarn

Für jeden Punkt im Datensatz wird die Menge seiner k-nächsten Nachbarn betrachtet. Diese Nachbarn werden durch gewichtete Kanten miteinander verbunden, wobei die Gewichte die (fuzzy) Distanzen zwischen den Punkten repräsentieren.

UMAP beginnt also damit, für jeden Punkt in den Daten eine Liste seiner nächsten Nachbarn zu erstellen. Hierbei wird oft der k-Nächste-Nachbarn-Algorithmus verwendet.

4. Distanzfunktion und Cross-Entropy

UMAP definiert eine spezielle Distanzfunktion, die dazu verwendet wird, die Ähnlichkeit zwischen den Punkten im hochdimensionalen und im niedrigerdimensionalen Raum zu messen. Die Distanzfunktion basiert auf der Cross-Entropy, einem Maß aus der Informationstheorie, das die Divergenz zwischen zwei Wahrscheinlichkeitsverteilungen quantifiziert.

UMAP versucht hierbei sowohl die lokale als auch die globale Struktur der Daten zu bewahren. Das bedeutet, dass sowohl nahe beieinander liegende als auch weit entfernte Punkte in den transformierten Daten in ähnlicher Weise positioniert werden.

5. Optimierung

Das Ziel von UMAP ist es, die Positionen der Punkte im niedrigerdimensionalen Raum so anzupassen, dass die Divergenz zwischen den Verteilungen der Distanzen im ursprünglichen und im projizierten Raum minimiert wird. Dies wird durch ein Optimierungsverfahren erreicht, typischerweise durch stochastische Gradientenabstieg.

Beispiel: Stellen Sie sich vor, Sie haben ein 3D-Modell einer Skulptur und möchten es in 2D darstellen. Sie müssen entscheiden, aus welchem Winkel Sie es betrachten, um die meisten Details zu erfassen.

6. Ergebnis

Das Ergebnis ist eine Darstellung der Daten im niedrigerdimensionalen Raum, die die topologische Struktur der ursprünglichen Daten so gut wie möglich bewahrt. Dies ermöglicht es, Muster und Strukturen in den Daten zu erkennen, die in höheren Dimensionen nicht sichtbar wären.

Unsupervised vs. Supervised UMAPing

Unsupervised UMAP

Der unsupervised UMAP, verwendet während des Prozesses der Dimensionsreduktion keine Label-Informationen. Er arbeitet ausschließlich basierend auf den Merkmalswerten der Daten. Das Ziel des Algorithmus ist es, eine niedrigdimensionale Darstellung der Daten zu finden, die die topologische Struktur so gut wie möglich bewahrt.

Supervised labeled UMAP

Supervised labeled UMAP hingegen integriert Label-Informationen (Welche zuvor in dem Datenset integriert sind) in den Prozess der Dimensionsreduktion. Die Hauptidee besteht darin, die Dimensionsreduktion so zu steuern, dass Datenpunkte mit denselben Labels im niedrigerdimensionalen Raum näher zusammengelegt werden, während solche mit unterschiedlichen Labels weiter auseinander liegen. Dies kann besonders nützlich sein, wenn Sie über ein gelabeltes Datenset verfügen und die Trennung zwischen verschiedenen Klassen visualisieren möchten oder wenn Sie UMAP für die Merkmalsextraktion verwenden möchten, um die Leistung eines überwachten Lernmodells zu verbessern.

Hauptunterschiede

Verwendung von Label-Informationen:
- Der „normale“ UMAP ist unsupervised und verwendet keine Label-Informationen.
- Supervised labeled UMAP verwendet Label-Informationen, um die Dimensionsreduktion zu steuern.
Zweck:
- Normaler UMAP wird hauptsächlich für die Visualisierung und Erforschung der intrinsischen Struktur der Daten verwendet.
- Supervised labeled UMAP kann auch für die Visualisierung verwendet werden, allerdings mit dem Fokus auf einer deutlichen Trennung zwischen verschiedenen Klassen. Er kann auch für die Merkmalsextraktion verwendet werden, um überwachte Lernaufgaben zu verbessern.
Resultierende Einbettung:
- Die durch „normalen“ UMAP erzeugte Einbettung trennt nicht notwendigerweise verschiedene Klassen gut, insbesondere wenn die Klassen im hochdimensionalen Raum nicht gut getrennt sind.
- Supervised labeled UMAP zielt darauf ab, eine Einbettung zu erzeugen, in der verschiedene Klassen deutlicher getrennt sind, was für Klassifizierungsaufgaben nützlicher sein kann.
Flexibilität:
- Normaler UMAP kann auf jedes Datenset angewendet werden, unabhängig davon, ob es gelabelt ist oder nicht.
- Überwachter gelabelter UMAP erfordert ein gelabeltes Datenset.

Wie kann der UMAP Algorithmus dies bewerkstelligen?

1. Konstruktion des Ähnlichkeitsgraphen:

Ähnlichkeit im hochdimensionalen Raum: Zuerst wird ein Ähnlichkeitsgraph im hochdimensionalen Raum erstellt – analog zu den Erläuterungen zu Beginn. Für jeden Punkt werden seine nächsten Nachbarn bestimmt, und eine gewichtete Kante wird zwischen ihnen erstellt. Die Gewichtungen basieren auf dem Abstand zwischen den Punkten, wobei nähere Punkte höhere Gewichtungen erhalten.
Label-Informationen: Die Labels werden dann verwendet, um diese Gewichtungen anzupassen. Wenn zwei Punkte das gleiche Label haben, wird ihre Verbindung im Ähnlichkeitsgraphen verstärkt, und das Gewicht der Kante zwischen ihnen erhöht. Im Gegensatz dazu wird die Verbindung zwischen zwei Punkten mit unterschiedlichen Labels geschwächt, und das Kantengewicht verringert.

2. Kreuzentropie-Minimierung:

Das Ziel von UMAP ist es, die Kreuzentropie zwischen den Verteilungen der Abstände im hochdimensionalen Raum und dem niedrigdimensionalen Raum zu minimieren.
Die Kreuzentropie-Verlustfunktion wird angepasst, um die Label-Informationen zu berücksichtigen. Dies geschieht typischerweise durch Modifizierung der anziehenden und abstoßenden Kräfte im Optimierungsprozess.
Anziehende Kräfte: Punkte mit demselben Label ziehen sich im niedrigdimensionalen Raum stärker an, was dazu führt, dass sie enge Cluster bilden.
Abstoßende Kräfte: Punkte mit unterschiedlichen Labels stoßen sich stärker ab, was dazu beiträgt, dass verschiedene Klassen in der Visualisierung getrennt werden.

3. Optimierung:

Die Positionen der Punkte im niedrigdimensionalen Raum werden iterativ angepasst, um den angepassten Kreuzentropie-Verlust zu minimieren.
Dieser Prozess wird fortgesetzt, bis sich die Einbettung stabilisiert hat, was zu einer Visualisierung führt, in der die lokale und globale Struktur der Daten erhalten bleibt und Punkte mit ähnlichen Labels zusammen gruppiert sind.

Mathematische Darstellung:

Sei 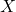$X$ die hochdimensionalen Daten und 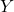$Y$ die niedrigdimensionale Darstellung.
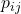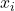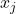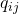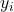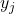Sei $p_{ij}$ die Ähnlichkeit zwischen den Punkten $x_i$ und $x_j$ im hochdimensionalen Raum, und sei $q_{ij}$ die Ähnlichkeit zwischen den Punkten $y_i$ und $y_j$ im niedrigdimensionalen Raum.
Die Kreuzentropie 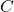$C$ zwischen den beiden Verteilungen kann wie folgt dargestellt werden:
$C = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}} + (1 - p_{ij}) \log \frac{1 - p_{ij}}{1 - q_{ij}}$
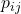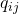Die Label-Informationen werden verwendet, um $p_{ij}$ und $q_{ij}$ anzupassen, Verbindungen basierend auf Label-Ähnlichkeit zu stärken oder zu schwächen.

Schlussfolgerung:

Mathematisch integriert der supervised UMAP die Label-Informationen, indem er die Gewichtungen im Ähnlichkeitsgraphen und die Kräfte im Optimierungsprozess anpasst, um sicherzustellen, dass Punkte mit den gleichen Labels näher zusammengezogen werden und Punkte mit unterschiedlichen Labels weiter auseinander gedrängt werden. Dies führt zu einer niedrigdimensionalen Darstellung, die besser mit der gelabelten Struktur der Daten übereinstimmt und interpretierbarere und aussagekräftigere Visualisierungen liefert.

Wie sieht eine einfache Umsetzung in Python aus?

import numpy as np
import matplotlib.pyplot as plt

# High-dimensional data (5 points in 3D space)
X = np.array([
    [1, 2, 3],
    [2, 3, 4],
    [3, 4, 5],
    [100, 100, 100],
    [101, 101, 101]
])

# Step 1: Choose Neighbors
neighbors = {i: np.argsort(np.sum((X[i] - X) ** 2, axis=1))[:2] for i in range(X.shape[0])}

# Step 2: Calculate Affinities
def affinity(x, y, sigma=1.0):
    return np.exp(-np.sum((x - y) ** 2) / (2.0 * sigma ** 2))

affinities = np.zeros((X.shape[0], X.shape[0]))
for i in range(X.shape[0]):
    for j in neighbors[i]:
        affinities[i, j] = affinity(X[i], X[j])

# Step 3: Initialize Low-Dimensional Representation
Y = np.random.rand(X.shape[0], 2)  # 2D space

# Step 4: Optimize Layout (Simplified)
# Here we'll use a very simple optimization approach for illustration
learning_rate = 0.01
for epoch in range(100):
    for i in range(X.shape[0]):
        for j in neighbors[i]:
            if i != j:
                # Attractive Force (proportional to affinity)
                gradient = 4 * (Y[i] - Y[j]) * (affinities[i, j] - 1 / (1 + np.sum((Y[i] - Y[j]) ** 2)))
                Y[i] -= learning_rate * gradient
                Y[j] += learning_rate * gradient

# Plotting the result
plt.scatter(Y[:, 0], Y[:, 1])
for i, txt in enumerate(range(X.shape[0])):
    plt.annotate(txt, (Y[i, 0], Y[i, 1]))
plt.show()

Wie sieht ein konkretes Beispiel aus?

In meinem Fall beziehe ich mich auf Daten aus einer Ganganalyse. Für jeden Patienten werden 105 Parameter erfasst, einschließlich des Labels. Dieses Label repräsentiert beispielsweise die Diagnose des Patienten. Unser Ziel war es nun, mit Hilfe von UMAP zu überprüfen, ob die von uns vergebenen Labels – die vorwiegend auf klinischen Einschätzungen basieren oder eine gesicherte Diagnose darstellen – durch dieses Set an Gangparametern ebenfalls zuverlässig klassifiziert werden können.

Der Python Code in vereinfachter Form:

# merge labels to umap_data
umap_data = pd.merge(umap_data, df_session_label, on="index")

# extract features only from umap_data
features = umap_data.drop(["index", "label"], axis=1)
features_scaled = StandardScaler().fit_transform(features)
# Set NaN to 0 after Scaling
features_scaled = np.nan_to_num(features_scaled)
# get idpatient
idgrtsession = umap_data["index"]
# get Labels
labels_string = umap_data["label"]
label_encoder = LabelEncoder()
y = label_encoder.fit_transform(labels_string)

umap_model = umap.UMAP(
    random_state=42,
    n_neighbors=15,
    min_dist=0.1,
    n_components=2,
    metric="euclidean",
    target_metric="categorical",
    target_weight=0.5,
)

if supervised:
    umap_result = umap_model.fit_transform(features_scaled, y)
else:
    umap_result = umap_model.fit_transform(features_scaled)

# Create a DataFrame with the UMAP results and labels
umap_df = pd.DataFrame(umap_result, columns=["UMAP_1", "UMAP_2"])
umap_df["Label"] = labels_string
umap_df["idgrtsession"] = idgrtsession

# Create the Plotly scatter plot
if supervised: 
    fig = px.scatter(
        umap_df,
        x="UMAP_1",
        y="UMAP_2",
        color="Label",
        color_discrete_sequence=px.colors.qualitative.Alphabet,
        title="UMAP",
        custom_data=["idgrtsession"],
    )
else:
    fig = px.scatter(
        umap_df,
        x="UMAP_1",
        y="UMAP_2",
        color="Label",
        color_discrete_sequence=px.colors.qualitative.Alphabet,
        title="UMAP",
        custom_data=["idgrtsession"],
    )
fig.update_layout(
    legend=dict(
        orientation="h", yanchor="bottom", y=1.02, xanchor="right", x=1
    )
)

Das Ergebnis unsupervised:

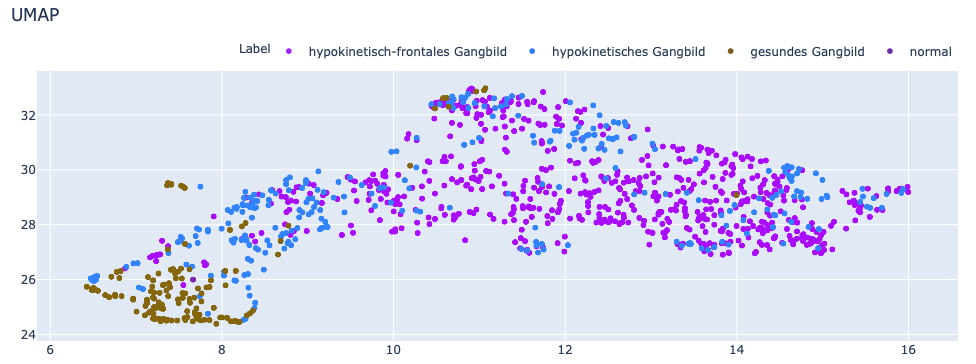
Die einzelnen Punkte sind zwar mit einem Label versehen, dieses wird jedoch nachträglich hinzugefügt und steht dem UMAP Algorithmus nicht zur Verfügung.

Das Ergebnis supervised:

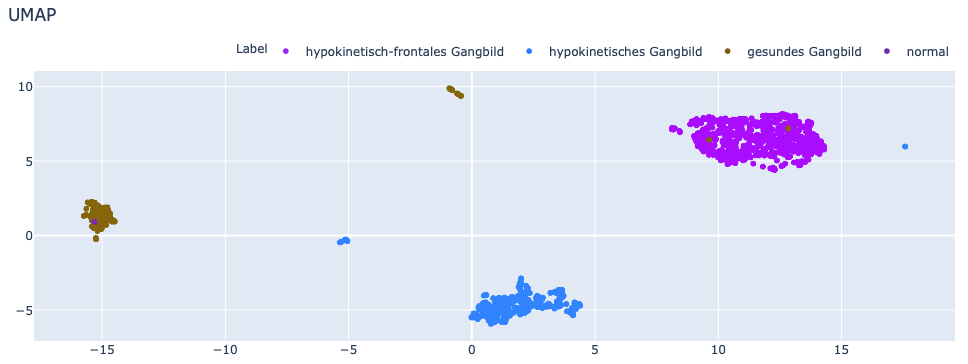
Dieses Bild hat ein leeres Alt-Attribut. Der Dateiname ist umap_supervised_1.png

Der Einfluss von Supervised Learning auf die Trennschärfe lässt sich anhand dieses Beispiels gut verdeutlichen.

UMAP – „Uniform Manifold Approximation and Projection“ und die Riemannschen Mannigfaltigkeiten

Write A Comment Cancel Reply